Повышение эффективности канальных кодеков ЦСП. Классификация методов канального цифрового преобразования, страница 22

В 1990 г. Объединенной группой экспертов в области фотографии (Joint Photographic Experts Group) был предложен алгоритм сжатия цветных неподвижных изображений, названный JPEG. Алгоритм включает несколько этапов обработки. На первом этапе цветные изображения, состоящие из трех цветоделенных изображений красного (R), зеленого (G) и синего (B) цветов, при последовательном считывании переводятся из пространства RGB в пространство YUV, где Y ≈0,3R + 0,59G + 0,11B — компонент яркости, U = R – Y, V = В –Y— цветоразностные компоненты. Цветовое пространство UV нe требует высокого пространственного разрешения из-за свойства зрения [12], поэтому на втором этапе выполняют операцию прореживания, когда отбрасывают (исключают из анализа как избыточные) отдельные строки и столбцы U- и V-компонентов. Обычно выполняется прореживание с коэффициентом 2:1:1, когда отбрасываются элементы (пикселы) цвета каждой второй строки и каждого второго столбца (или на два отсчета сигнала Y берутся по одному отсчету сигналов V и U).

На третьем этапе каждое двумерное пространство пикселов Y, Uи V по отдельности подвергается спектральному преобразованию по методу дискретного косинусного преобразования (ДКП). Обработка ведется блоками N×N пикселов, где N = 8, т.е. по 8 элементов в 8 соседних строках. Расчет спектральных коэффициентов производится по аналогии с (14.35), при этом интенсивность цвета (или яркости) L(p, q) в точке с координатами р, q, где р, q  [0, N–1], связана с величиной спектрального коэффициента S_mn выражениями

;

;

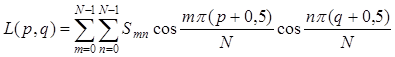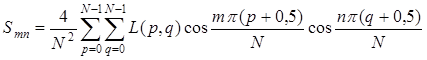.                                (14.41)

Матрица коэффициентов S_mn отражает амплитуды пространственных частот в изображении L(p, q), при этом максимальные коэффициенты, которые характеризуют низкие пространственные частоты, расположены в верхнем левом углу матрицы N×N, а минимальные, соответствующие верхним пространственным частотам, — в правом нижнем.

На четвертом этапе производится «отбрасывание» (фильтрация) малых коэффициентов S_mn и кодирование оставшихся. Фильтрация может быть фиксированной, например, по правилу «зоны»: исключаются («обнуляются») коэффициенты, для которых (п + т) > k, где k — заранее выбранное число, или по правилу «порога»: отбрасываются те коэффициенты, которые меньше максимального коэффициента в определенное l число раз. Как правило, при N = 8 в матрице остается от 3 до 10 коэффициентов. Квантование и кодирование оставшихся коэффициентов осуществляется по-разному в зависимости от частоты их появления: часто встречающиеся коэффициенты (обычно с малым значением n и m) кодируются более короткими кодовыми комбинациями, редко встречающиеся — более длинными. Такое кодирование символами переменной длины называется кодированием по Хаффмену. Оно позволяет уменьшить среднюю длину кодовой последовательности для передачи спектральных коэффициентов. Отметим также, что квантование U- и V-составляющих выполняется более грубо.

Определим ориентировочно эффективность кодирования по алгоритму JPEG для передачи цветного неподвижного изображения, содержащего N_ээлементов (пиксел) по строке и N_cстрок. При обычном кодировании на передачу одного изображения потребовалось бы N_Σ2 = N_эN_c(m_Y + т_U + т_V), бит, где обычно т_Y= 8, т_U= т_V= 4.

При эффективном кодировании в режиме 2:1:1 требуется

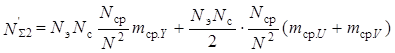, где N = 8; N_cp— среднее число учитываемых спектральных коэффициентов в матрице n ×N; т_ср.Y, m_cp.U, m_cр.V — среднее число бит на один отсчет спектрального коэффициента для Y-, U- и V-составляюших.

Полагая N_cp≈8; т_ср.Y= 6; m_ср.U= т_ср.V= 3, найдем коэффициент сжатия объема изображения:

.

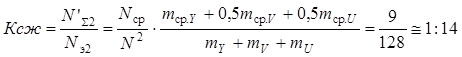При таком сжатии передача цветного изображения формата А4 в течение 1 мин с разрешением порядка 600 × 900 пиксел потребует цифрового канала со скоростью передачи С_к = N'_э2/60≈11 кбит/с.

Для сжатия подвижных (например, телевизионных) изображений алгоритм JPEG этой же группой разработчиков был несколько модернизирован и приведен к варианту Motion JPEG(MJPEG). Для него при передаче N_Kкадров в секунду и сохранении тех же параметров кадра, что и в алгоритме JPEG, требуется цифровой канал со скоростью передачи С_к = N'_Σ2N_к= 16 Мбит/с.