Затем цифровой сигнал проходит по цифровому тракту и попадает в приемную часть, где декодируется в декодере 4 по линейному или нелинейному закону цифро-аналогового преобразования. Разностный сигнал ∆U'j}, который отличается от сигнала ∆Uj на величину ошибки квантования, поступает в сумматор 5. На второй вход его поступает сигнал предсказания U'пр.j, который формируется в предсказателе 6 по такому же алгоритму, как и в предсказателе I, т.е. по совокупности предыдущих значений выходного сигнала U'. При этом
U'j = U'пр.j + ∆U'j. (14.2)
Равенство (14.2) с точностью до ошибки квантования совпадает с (14.1). Это позволяет формировать сигнал предсказания в передающей части по такому же алгоритму, как и в приемной. Тогда приходим к схеме рис. 14.2, которая характеризует кодер ДИКМ с декодером в цепи обратной связи (обозначения блоков здесь такие же, как на рис. 14.1). Такая схема имеет следующие преимущества:
1) 
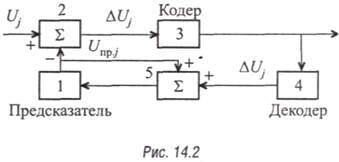идентичность
предсказаний повышает качество восстанавливаемого сигнала;
2) случайные сбои в работе кодера 3 исправляются («отслеживаются») на последующих шагах;
3) упрощаются требования к точности получения взаимосвязанных характеристик нелинейных кодеров и декодеров;
4) не происходит накопления ошибки квантования.
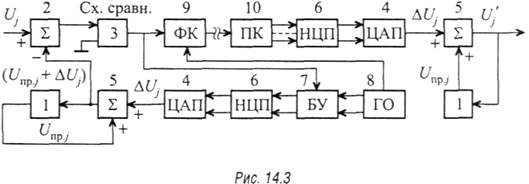
Если кодер 3 на рис. 14.2 строить по схеме, например, взвешивающего нелинейного кодера с декодером в цепи обратной связи (см. рис. 13.54), то схема кодера ДИКМ приведется к более простому виду (рис. 14.3). Здесь блоки 1, 2 и 5 выполняют те же функции, что и одноименные блоки на рис. 14.2. При этом нелинейный декодер содержит известные блоки нелинейного цифрового преобразователя (НЦП) 6 и линейного цифро-аналогового преобразователя (ЦАП) 4. На выходе ЦАП в процессе взвешивания, осуществляемого с помощью известных блока управления (БУ) 7 и генераторного оборудования (ГО) 8 (см. подпараграф 13.3.5), формируется напряжение ∆Uj такой величины и знака, чтобы с точностью до ошибки квантования выполнялось условие: Uj – Unp.j + ∆Uj ≈ 0. Процесс взвешивания контролируется схемой сравнения (Сх.сравн.) 3, второй вход которой имеет нулевой потенциал. Формирователь кода (ФК) 9 известным образом формирует кодовую комбинацию, соответствующую величине ∆Uj. При отсутствии НЦП 6 квантование ∆Ujпроизводится, очевидно, с постоянным шагом квантования и соответственно линейным кодированием. На приемной стороне преобразования производятся в обратном порядке, только предварительно преобразователь кода 10 формирует цифровую комбинацию, соответствующую ∆Uj, в параллельном коде. Возможны различные варианты построения предсказателя, которые отличаются видом функциональной связи напряжения сигнала в момент t= t0 + ∆tс параметрами сигнала в момент t0.
1. Предсказание первого порядка:
Uпр(t) = Uпр(t0 + ∆t) или Unp.j = Uj–1. (14.3)
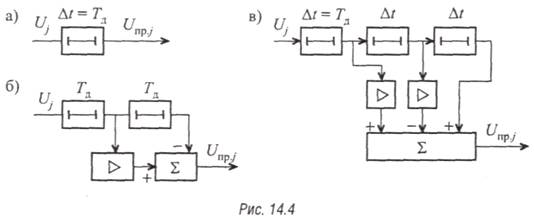
Предсказатель по алгоритму (14.3) содержит линию задержки (ЛЗ) на время Тд (рис. 14.4, а).
2. Предсказание второго порядка:
.
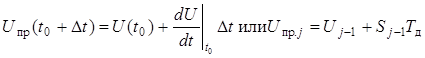Поскольку это предсказание справедливо и для предыдущей точки, т.е. для ∆t = –Тд, значение в которой известно и равно Uj–2, получим Uj–2 = Uj–1 – Sj–1Tд,откуда Sj–1 = (Uj–1 – Uj–2)/Tд. Тогда
. (14.4)
Предсказатель, реализующий (14.4), содержит две ЛЗ, усилитель с коэффициентом усиления 2 и схему вычитания (рис. 14.4, б).
3. Предсказание третьего порядка:
,
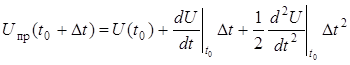Uпр.j = Uj–1 + Sj–1Tд + 0,5S'j-1Tд2.
Используем это уравнение для моментов ∆t = –Tд и ∆t = –2Tд, когда предсказанные значения точно известны и равны Uj–2 и Uj–3. Тогда
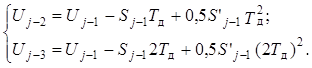
Решаем эти уравнения относительно неизвестных Sj–1, S'j–1и получаем
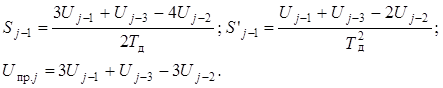(14.5)
Предсказатель, построенный по (14.5), показан на рис. 14.4, в. Используя (14.3) —(14.5), предсказанное значение Unp.jможно записать в виде
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.