Теория дискретных систем автоматического управления: Учебное пособие. Часть IV: Нелинейные системы

удк 65.011.56 (075.8) БЖ 32.815

Рецензенты: ЮМ. Астапов, Ю. В. ПоДуриев

Иванов В,А., Голованов МА.

ид) Геория дискретных систем автоматического управления: Учеб- пособие, Ч. IV: Нелинейные системы: — М.: Изд-во РИГГУ им- П Баумана, 2003. — 56 с.: ил.

lSllN  О

В учебном методы анализа нелинейных дискретных автомал ическп.ч н--м Рассмотрены метод фазовой плоскости, исследование .щпск•рс [ПЫХ систем с помотцью прямого метода

                                           ДИСК Ре              СИСЛГМ

п 1 га ППфРOНЫ,Ч атома 1 иче.ских систем». Ил р •l iinan удк 65.011.56 (075.8)

ББК 32.815

ISBN 5-7038-2308-0                                                        М! У им. Н.Э. Баумана, 2003

1. МЕТОД ФАЗОВОЙ ПЛОСКОСТИ

1.1. Основные понятия и определения

Рассмотрим автономную систему разностных уравнений д-Х1 [П] = Л (Ч Х2 [П] д.Х2 [П] = f2(X1 [П], Х2 [П]

(1.1)

                                  Ахк [п] = fk („Ч         X2[nl,

Систему (1.1) можно записать в векторном виде дх[п]

где

                         дх[п] =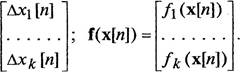                 (1.2)

Полагаем, что правые части системы уравнений (1.1) непрерывны, ограничены и однозначны в выпуклой области G К-мерного пространства Х. Это обеспечивает существование и единственность решения системы уравнений (1.1)

Решения автономной системы (1.1) обладают следующим важным свойством: если имеется некоторое решение Xi (i 1,2,..., К) системы (1.1), то функции Xi

(i - 1,2, К) , где I = const, также представляют собой решение системы (1.1).

В самом деле, так как Xi = [п] (i = 1,2,..., К) — решение системы (1.1), то имеют место тождества [п] = [п], Ц2[п]

(i - 1 2                   К). Заменив в этих тождествах п на п + 1, получим

                                      +1],                             а [п + 11) (i            1,2             К). но

Ц [п + 1]                + + 1] —           + 1] = Ei[n + 1] — Ei[nl = дЧ[п]. Тогда

                                                      Е2[п],                                                              (1.3)

Дадим геометрическую интерпретацию решений автономной системы. Рассмотрим К-мерное пространство Х с кординатами  хк. Пусть .Xi = % [п] (i= 1,2,..., К) — некоторое решение системы (1.1). Каждому фиксированному значению п соответствует точка в пространстве Х, называемая изображающей точкой. При изменении п от —сп до оо изображающая точка пробегает последовательность дискретных точек, образующих фазовую траекторию.

Пространство Хназывается фазовым  Можно показать, что различным решениям системы ( I 1)фазовые траектории, которые либо не имеют общих либо совпадают.

Назовем состоянием равновесия системы разносл пых уравнений (1.1) фазовую траекторию, соответствующую решению

Xi[nl = ај (i — 1,2,... К)

Состояние равновесия представляет собой решение системы уравнений

                                                      (1.5)

полученных из системы (1 1 ) путем  Н УЛ ю ЛСВЫХ частей.

В самом деле, если

(i  К), [1 система уравнений (1 1) принимает вид (1.5).

1.2. СОСтОЯния равновесия системы линейных разностных уравнений

второго порядка

Рассмотрим автономную систему разностных уравнений второго порядка

                                                             (1.6)

Пусть Xi[nl = ај (i = 1,2) — некоторое состояние равновесия системы (1.6). Для исследования поведения фазовых траекторий в некоторой окрестности состояния равновесия составим уравнения для отклонений. Для этого перейдем к переменным и [п] а1 и Y2[nl = Х2[п] 02. Учитывая, что дул [п] = д.Х1 [п], Дк [п] = дх2[п], получим следующую систему уравнений для отклонений:

Разложим правые части этих уравнений в ряд Тейлора в окрестности состояния равновесия (щ 02) и 0l рапичИМСЯ линейными членами разложения. Для состояния равновесия справедливы ра4

венстваЛ(аг, ) = 0, f2(a1, а2 ) = 0, поэтому получим следующую систему линейного приближения для отклонений от состояния равновесия:

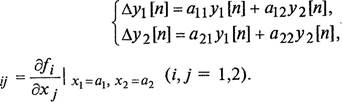(1.7)

где а

Систему разностных уравнений (1.7) запишем в векторном виде ду[п] = Ау[п],  (1.8)

где ду[п] —y[ⁿl =

⁰ 21 ^а п

Система уравнений линейного приближения справедлива в некоторой малой окрестности состояния равновесия. Однако известны случаи, когда система линейных разностных уравнений вида (1.7) описывает динамику дискретной автоматической системы. Поэтому исследование фазовых траекторий линейной системы второго порядка имеет и самостоятельное значение.