Теория дискретных систем автоматического управления: Учебное пособие. Часть IV: Нелинейные системы, страница 10

Таким образом, достаточное условие абсолютной устойчивости состояния равновесия для дискретной системы с устойчивой дискретной линейной частью и нелинейной характекристикой, удовлетворяющей условиям состоит в положительности вещественной части функции Н (Д), называемой дискретной функцией Пбпова:

 (2.38) К

С помощью неравенства (2.38) можно определить величину сектора (0, К) , в котором должна находиться статическая характеристика нелинейного элемента, чтобы нелинейная дискретная система была абсолютно устойчива.

Из условия (2.38) следует, что нелинейная дискретная система абсолютно устойчива, если частотная характеристика И/ (16) линеЙноЙ дискретной части расположена на комплексной плоскости правее вертикальной прямой —1/k. На рис. 24 изображена частотная характеристика (Д) линейной дискретной части для абсолютно устойчивой нелинейной дискретной системы. При этом характеристика нелинейного элемента должна располагаться в секторе (0, К) (рис. 25). Критическое значение коэффициента К Ко, определяющее наибольший сектор, внутри которого должна находиться статическая характеристика нелинейного элемента у , можно найти из условия касания частотной • характеристики и прямой —1/Ко (рис. 24).

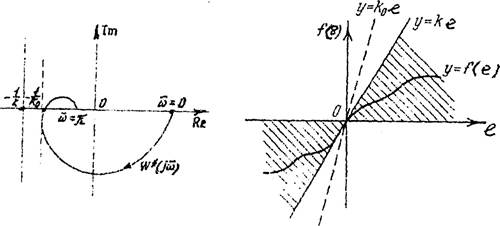
                          Рис. 24                                                        Рис. 25

35

Абсолютная устойчивость систем с нейтральной или неустойчивой линейной частью. Рассмотрим нелинейную дискретную систему с неустойчивой или нейтральной линейной частью. Для такой системы передаточная функция (q) имеет полюсы, расположенные либо в правой полуполосе, либо на мнимой оси: Re 0, —л < Imq л. Охватим неустойчивую линейную дискретную часть системы жесткой отрицательной обратной связью с коэффициентом Кг в цепи обратной связи. При этом коэффициент kl выберем таким образом, чтобы в целом линейная дискретная часть стала устойчивой, т. е. чтобы все полюсы передаточной функции

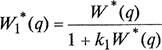                                                                    (2.39)

расположились в левой полуполосе: Re < 0, —л < Jmq л. Структурная схема этой системы показана на рис. 26 (НЛДЧ — неустойчивая линейная дискретная часть).

Для того чтобы дискретная система, у которой дискретная линейная часть охвачена отрицательной обратной связью, была эквивалентна исходной системе, необходимо охватить нелинейный элемент прямой отрицательной связью с коэффициентом усиления kl (см. рис. 26). Отметим, что эквивалентность исходной нелинейной дискретной системы и нелинейной дискретной системы, изображенной на рис. 26, имеет место только при входном воздействии g[nl = 0. Статическую характеристику f1(e) нелинейного элемента с учетом прямой отрицательной связи запишем в видеЛ(е) =f(e) — Че, где Ле) — статическая характеристика нелинейного элемента, не охваченного прямой отрицательной связью.

Для нелинейной дискретной системы с устойчивой линейной дискретной частью, характеризуемой передаточной функцией W1 (q) и нелинейным элементом, имеющим статическую характеристикуЛ(е), применимы полученные выше результаты. Эта сис-

36

тема будет иметь абсолютно устойчивое состояние равновесия, если характеристика нелинейного элемента удовлетворяет условию

или kl  +kl =k,       (2.40)

а частотная характеристика И/1 (Д) располагается правее вертикальной прямой —l/k2 для всех значений б е [0, п], т. е. для всех значений должно быть справедливо неравенство

                                                                   (2.41)

Для систем с астатической непрерывной линейной частью, передаточная функция которой имеет полюсы в начале координат и в левой полуплоскости, величина коэффициента kl может быть выбрана сколь угодно малой. В общем случае коэффициент К1 может быть и отрицательным числом (рис. 27).

Рассмотрим способ исследования абсолютной устойчивости нелинейной дискретной системы, основанный на использовании амплитудно-фазовой частотной характеристики и^х (16) дискретной линейной части исходной системы [З]. Подставим в формулу (2.41) значение из (2.39). Учитывая, что К2 = К — kl, получаем следующее неравенство: