Теория дискретных систем автоматического управления: Учебное пособие. Часть IV: Нелинейные системы, страница 15

где Ко — коэффициент усиления; р = —; 7'l — постоянная времени звена.

Ей соответствует частотная характеристика линейной дискретной системы

нелинейность  описывается    релейной         характеристикой Q(6) = sign о.

Качественный вид частотных характеристик W(jo) и показан на рис. 34.

Согласно (З. 19), выражения для коэффициента гармонической линеаризации нелинейного импульсного элемента типа идеального реле имеют следующий вид:

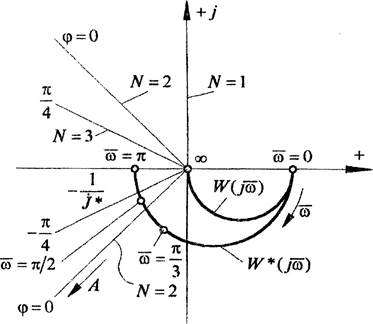
Рис. 34

51

для четных л^т

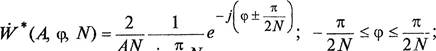
sin — л^т 2

для нечетных л^т е—Јр .

АЛ^Г . п sm

Найдем возможные решения уравнения гармонического баланса системы в форме (3.21). Для этого на плоскости частотных характеристик (см. рис. 34) изобразим семейство графиков для различных л^к.

1

и, как следует из рис. 34, такой режим в рассматриваемой системе возникает всегда.

В ситуации, представленной на ис. 34, в соответствующий сектор попадает еще точка и^д у— частотной характеристики 2

И⁷ (Д). Это означает, что в системе существует устойчивый периодический режим с полупериодом л^т = 2-

Других периодических режимов с большим полупериодом л^т

данная система не имеет.

Метод гармонической линеаризации для дискретных систем с  использованием логарифмических частотных характеристик (ЛМ) аналогичен соответствующему методу для непрерывных систем. Задача сводится к решению следующих уравнений, полученных из (3.20):

 (Р, ЛЭ =LmWv7 j—tg—

и

J—tg——

52

20	дБ -LmWH(a, 2,  -1
	lga 10	lg a

(Р)

-1

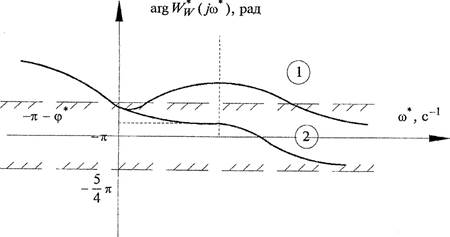
Рис. 35

В качестве примера определим методом ЛЧХ автоколебания, соответствующие л^к = 2 в дискретной системе с заданными логарифмическими амплитудными частотными характеристиками и логарифмическими фазовыми частотными характеристиками (см. рис. 34). Нелинейный элемент имеет релейную характеристику (см. рис. 32), То с.

2, =201g

53

4

                        — Л л                                  2       л             2-1

      Значению     = — соответствует 00* = ——tg

                               2                                     то 2N то

Если при этой частоте фазочастотная характеристика (Р(о) = = argW (јо) не заходит в заштрихованную область (кривая 1 на рис. 35), то автоколебаний при N= 2 нет; в противном случае из графиков (Д 2, ф) можно найти амплитуду и фазу (Р автоколебаний.

Список литературы

1.  Математические основы аавтоматического регулирования. В 2 т. Т. 1, 2 [Иванов ВЛ., Медведев ВС., Чемоданов БК. , Ющенко АС. М.: Высш. шк., 1977.

2.  Попов Е.П. Теория нелинейных систем автоматического ре-

гулирования и управления. М.: Наука, 1979.

З. Цыпкин ЯЗ, Попков Ю. С. Теория нелинейных импульсных систем. М.: Наука, 1973.

4. Шамриков ЛМ. Основы теории цифровых систем управления: Учебник для высших технических учебных заведений. М.: Машиностроение, 1985.

Оглавление

1.  Метод фазовой плоскости

1.1.  Основные понятия и определения.

1.2.  Состояния равновесия системы линейных разностных уравнений второго порядка  4 2. Анализ устойчивости нелинейных дискретных систем 23

      201. Основные понятия и определения                                                            23

      2.2. Теоремы Ляпунова об устойчивости и неустойчивости                           24

2.3. Исследование устой^кшвости по уравнениям линейного приближения 27

2.4. Геометрический критерий абсолютной устойчивости ,щскретных систем31 З. Метод гармонической линеаризации в теории дискретных систем40

3.1. Коэффициенты гармонической линеаризации42

3.2. Определение параметров периодических решений47 Список литературы.         54

Виктор Александрович Иванов

Михаил Алексеевич Голованов

ТЕОРИЯ ДИСКРЕТНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Часть IV

Нелинейные системы

Редактор ОМ. Королева

Корректор Л,И. Малютина

Подписано в печать 14.05.03. Формат 60х84/16. Бумага офсетная. Печ. л. 3,5. Усл. печ. л. 3,25. Уч.-изд. л. 3,15. Тираж 100 экз. Изд. № 82. Заказ“

 Издательство МГЛУ им. Н.Э. Баумана. 105005, Москва, 2-я Бауманская, 5.