Теория дискретных систем автоматического управления: Учебное пособие. Часть IV: Нелинейные системы, страница 9

2.4. Геометрический критерий абсолютной устойчивости дискретных систем

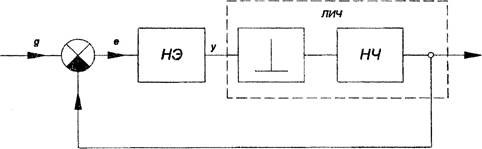
Абсолютная устойчивость систем с устойчивой линейной частыо. Рассмотрим дискретную автоматическую систему, структурная схема которой может быть приведена к виду, указанному на рис. 23, где НЭ — нелинейный элемент, который полагается безынерционным; ЛИЧ — линейная импульсная часть; НЧ непрерыная часть. Обозначим импульсную переходную функцию линейной импульсной части И'п[п, 0]. Тогда в силу устойчивости линейной импульсной части lim wrr [п, 0] = 0.

Статическая характеристика у = Ле) нелинейного элемента удовлетворяет следующим условиям:

Ле)

                                                                                      (2.23)

где К > 0 — некоторое постоянное число.

31

Рис. 23

Состояние равновесия дискретной системы абсолютно устойЧИВО, если оно устойчиво в целом, т. е. при любых начальных отклонениях, для произвольной нелинейной характеристики, удовлетворяющей условиям (2.23).

Определим достаточное условие абсолютной устойчивости для рассматриваемого класса нелинейных дискретных систем. Уравнение, описывающее поведение дискретной системы, имеет вид

                              = g[BOl — Е wn[n — 0]) .                     (2.24)

Входное воздействие g[n, 0] полагаем либо постоянным, либо исчезающим, т. е.

lim g[n, О]

П 00

Тогда для абсолютной устойчивости состояния равновесия необходимо и достаточно, чтобы

lim е[п, 0]

П ОО

Применим к обеим частям равенства (2.24) дискретное преобразование Лапласа. Получим

                                            (2.25)

где D — символ дискретного преобразования Лапласа. Линейная дискретная часть системы по предположению устойчива, поэтому все полюсы передаточной ФУНКЦИИ W(q) расположены в левой полуполосе, т. е. удовлетворяют условию Re qj < 0, —л Тт qj п (i  s). Введем вспомогательные функции если 0 S п

(2.26)

0, если п sO, п

и

                                              УГ [^п]                - (Pr [^пу^к ,                                    (2.27)

где er[nl               Е И'п (п -(2.28)

Для значений п, удовлетворяющих неравенству 0 s п r, справедливо er[nl = e(nl. Образуем следующее выражение:

32

                                                                     (2.29)

Учитывая равенства (2.26) и (2.27), получаем

Применив к равенству (2.29) формулу Парсеваля, найдем

(2.30)

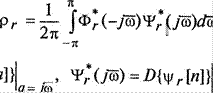где (Д) = D{Qr [nl}l

q=J0

Принимая во внимание формулы (2.27) и (2.28), получаем

                       Wr(J6) =                - ФДјб) - +                (2.31)

Подставим выражение (2.31) в формулу (2.30), тогда

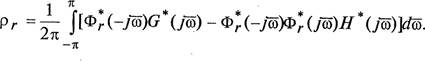
Здесь

                                                                (2.32)

Напишем два очевидных равенства. Вначале, заменив частоту о на = —6, получим

(2.33)

—л

Затем, учитывая, что вещественная часть функции Н (Д)

ReH (16) Щ (б) — четная функция частоты б, а ее мнимая часть Тт Н (16) = Н 2 (б) — функция нечетная, найдем

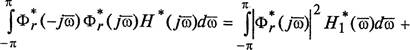
33

+ј (2.34)

                                   —л                                                        —л

Принимая во внимание равенства (2.33) и (2.34), преобразуем выражение (2.32):

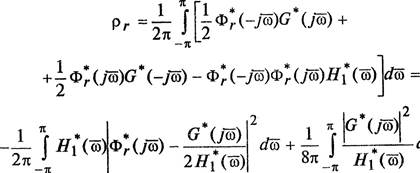б. (2.35)

— тс

Полагаем теперь, что имеет место неравенство

для всех б е [—ть тс]. Тогда левая часть равенства (2.35) преобразуется к виду

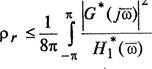2 d6=q,

причем ст > 0. Таким образом, для любого r > 0 справедливо нера-

                                        — f(elnl)            . Это неравенство означает, венство 1

keinl

что последовательность частичных сумм ряда

                                                             (2.36)

ограничена; следовательно, ряд (2.36) сходится. Из сходимости ряда с неотрицательными членами следует, что предел общего члена ряда

                                -0.                      (2.37)

Если учесть свойства нелинейной характеристики у = Ле), то из равенства (2.37) следует, что lim е[п] = 0. Абсолютная устойчи-

П СО

вость состояния равновесия доказана.

34