Теория дискретных систем автоматического управления: Учебное пособие. Часть IV: Нелинейные системы, страница 4

Если = 1, то уравнения (1.23) принимают вид q[nl — Ср Z2[nl = —С2е ^Т2П Фазовые траектории для этого случая при < 1 приведены на рис. 12. Если t2l = 1, то уравнения фазовых траекторий будут [п] = сте ^ТР , Z2[nl  Фазовые траектории для этого состояния равновесия показаны на рис. 13 для случая; когда

13

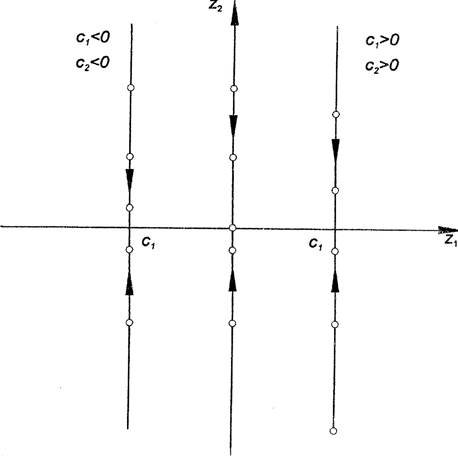
Рис. 12

Случай 4. Характеристические числа r и комплексные: , где у = — а ² + р ² , 0 =argn, COSQ =

— ос/у, sin(P = Му .

Тогда уравнения для фазовых траекторий запишутся в виде

[п] = у^п (q cosnq) + c2 sinnqo) =

= у^п (Ч [0] cosnp —            sinnp), Z2[nl = у ^п (—с2 cosno + sinnp) =

(1.27)

= уп (Z 2 [0] cosnq + [01 sinno),

14

или

[п] = Ау^л cos (тр + б), Z2[n] = Ау ^п + б), где А = Zl [012 + Z2[012 cos = [О]/А, sin6 = (2 [О]/А.

Для дальнейшего изложения удобно записать уравнения (1.27) фазовых траекторий в полярных координатах р и у:

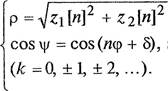= Ау ^п siny = sin(mp + б), = тр + 6+ 2Кп

Получим уравнение фазовых кривых. Имеем п = (у — 6 — 2Кл)Вр, тогда

                                    (1.28)

Если у                                     то lim р[п] = О, и состояние равновесия называется устойчивым фокусом. Фазовые траектории для этого случая приведены на рис. 14, а.

Если у                                     то lim р[п] = 00,

00

и состояние равновесия называется неустойчивым фокусом. Фазовые траектории для неустойчивого фокуса указаны на рис 14, б.

Пусть теперь у = 1. В этом случае переход из одного состояния в другое осуществляется путем поворота радиуса-вектора р посто15

Рис. 14

янной длины на угол (Р = arg Таким образом, точки фазовой траектории расположены в вершинах многоугольника. Если существует такое целое число l, что ф = 2Кп, этот многоугольник замкнут. Фазовые кривые представляют собой окружности радиуса р[0]. Состояние равновесия называется вершиной (рис. 15).

16

Случай 5. Характеристические числа и r2 совпадают, т. е. — — r. Тогда система разностных уравнений приводится либо к виду (1.16), либо к (1.17).

Общее решение системы (1.16) будет:

Zl[nl

Исключив время п, получим уравнение фазовых кривых ф cq. Фазовые кривые представляют собой прямые линии, проходящие через начало координат.

Пусть теперь r > 0. Фазовые траектории — последовательности точек на прямых линиях, проходящих через начало координат. Если r< 1, то lim [п] = lim Z2[n]

                                                          П ОО                        П 00

Состояние равновесия называется устойчивым Декритическим узлом 1-го типа. Если r > 1, то последовательности точек будут расходиться. Состояние равновесия называется неустойчивым Декритическим узлом 1-го типа. Фазовые траектории для устойчивого декритического узла 1-го типа показаны на рис. 16.

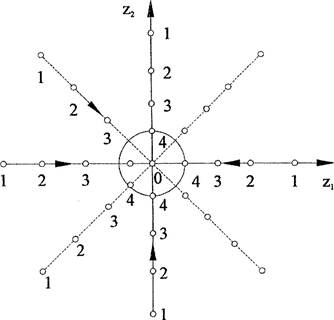
Рис. 16

17

Если r < О, то решение (1.19) можно записать в виде q[nl — = rlⁿ, Z2[nl = r р. Фазовые траектории, как и в предыдущем случае, представляют собой последовательности точек, расположенных на прямых линиях, проходящих через начало координат. Состояние равновесия называется устойчивым декритическим узлом 2-го типа, если r > —1, и неустойчивым Декритичесим узлом 2-го типа, если r < —1. Фазовые траектории для устойчивого декритического узла 2-го типа показаны на рис. 17.

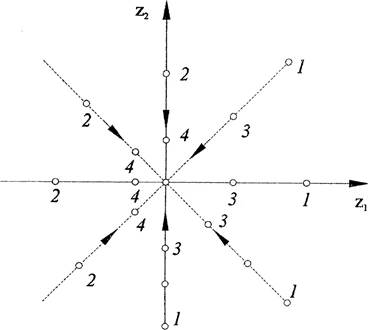
Рис. 17

Пусть теперь исходная система уравнений приведена к виду

(1.17). Ее общее решение, согласно (1.20), будет [п] = + , Z2[n] =С2Р

Если r > О, то общее решение (1.20) можно записать так:

                              ч [п] = е ТП         + 9.211 , Z2[nl =С2етп

где т = lnr. Исключив время п, получим уравнение фазовых кривых

⁵² + ——ln

18

        При 1'                lim [п] = lim Z2[nl

П 00

Состояние равновесия называется устойчивым вырожденным узлом 1-го типа, При r > 1 состояние равновесия представляет собой неустойчивый вырожденный узел 1-го типа. Фазовые траектории для устойчивого и неустойчивого вырожденных узлов 1-го типа показаны на рис. 18.

Если r < 0, то решение (1.20) можно записать в виде

                      [п]               |rlⁿ              + ⁹.²-n , Z2[n]

или