Теория дискретных систем автоматического управления: Учебное пособие. Часть IV: Нелинейные системы, страница 8

                                                х = Ту.                                        (2.12)

Тогда система уравнений (2.8) преобразуется к виду + = r ^l PTy[nl + Т-1

                                   + Ц = ^л у[^п] +                                      (213)

где = Т  Из равенств (2.11) следует, что компоненты rli(y) векторной функции тт(у) удовлетворяют равенствам

(2.14)

Матрица Т в преобразовании переменных (2.12) невырожденная, поэтому исследование асимптотической устойчивости тривиального решения системы (2.8) сводится к исследованию асимптотической устойчивости тривиального решения системы (2.13).

Выберем функцию Ляпунова в виде

К

Ку) = ElYil2(2.15)

28

где у* = Л,  = У ^Т . Функция V(y), задаваемая формулой (2.15), будет определенно-положительной. Покажем, что первая разность этой функции в силу системы уравнений (2.13) представляет собой определенно-отрицательную функцию. Составим выражение для первой разности:

                          =          + lly[n + 11 - ут           =

      = у ^т [ⁿl(¹ Л -      +

Выполним оценку отдельных слагаемых, входящих в выражение для первой разности.

Для первого слагаемого

К

Если обозначить min(1 -- liil ² ) = а, то, учитывая, что             для всех

i = 1, 2,..., К, получим ос > 0. Тогда для первого слагаемого справедливо неравенство

                                                (2.16)

причем > О — указанное выше число. Из равенств (2.14) следует, что для любого сколь угодно малого Е > 0 существует такое число h > 0, что < ellyll, если llyll <h. Тогда для второго слагаемого

Если llyll <h, то, учйтывая предыдущее неравенство, можно записать

                                      ^Ellyllⁱmax E W ⁱ b                              (2.17)

где Х          = тах liil. Используя неравенство Гельдера, получаем

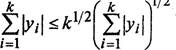                                    = kl/2|lyll•                           (2.18)

Из (2.17) и (2.18) найдем следующую оценку для второго слагаемого:

29

                                              (2.19)

Аналогичная оценка может быть получена для третьего слагаемого: у ^т  Таким образом, из неравенств (2.16) и (2.19) следует, что первая разность дЦу[п]) удовлетворяет неравенству

                         д                 -ка -28               (2.20)

Число Е может быть выбрано сколь угодно малым. Согласно формуле (2.20), это означает, что существует такая /1-окрестность начала координат, в которой первая разность  будет определенно-отрицательной функцией. Таким образом, построена определенно-положительная функция первая разность которой в силу системы уравнений (2.13) прдставляет собой определенно-отрицательную функцию. Согласно теореме 2.2, это означает, что тривиальное решение системы уравнений (2.13), а, следовательно, и тривиальное решение системы уравнений (2.8) асимптотически устойчиво.

Приведем без доказательства теорему о неустойчивости тривиального решения системы уравнений (2.8)

Теорема 2.5. Если хотя бы один корень характеристического уравнения матрицы Р расположен вне единичного круга, т. е. хотя бы для одного ii имеет место неравенство liil > 1, то тривиальное решение системы уравнений (2.8) неустойчиво.

Ерли среди корней характеристического уравнения имеются корни, расположенные на окружности единичного радиуса, т. е. корни с модулем, равным единице, то по уравнениям линейного приближения нельзя судить об устойчивости тривиального решения нелинейной системы разностных уравнений. В этом случае, называемом критическим, устойчивость тривиального решения зависит от нелинейной части

Пример. Исследовать устойчивость тривиального решения системы разностных уравнений

+ 1] =

(2.21)

Разложим функцию sin у в ряд Маклорена sin у = Е

Тогда система уравнений линейного приближения для системы

(2.21) будет иметь вид

+ y[nl,

(2.22)

Матрица Р системы уравнений (2.21) будет Р =     коро -1,5 ни характеристического уравнения матрицы Р det[P — ЛЕ]

                             = 7? + Х--@75 равны i1 = —1,5; 12 = 0,5. Один корень расположен вне единичного круга (li1 I > 1), поэтому тривиальное решение системы уравнений (2.21) неустойчиво.