Теория дискретных систем автоматического управления: Учебное пособие. Часть IV: Нелинейные системы, страница 11

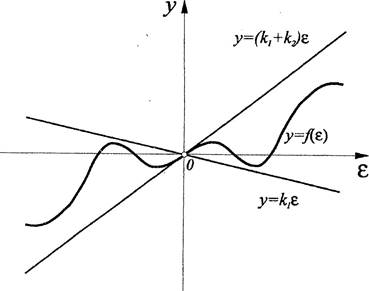
Рис. 27

37

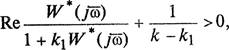
или

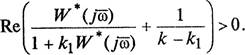
Принимая во внимание, что К — kl > 0, находим

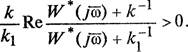                                                               (2.42)

В зависимости от знака коэффициента К неравенство (2.42) эквивалентно либо неравенству

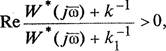                                                                   (2.43)

если > О, либо неравенству

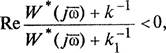                                                                   (2.44)

если К1 < О.

Найдем геометрическое место точек на комплексной плоскости, удовлетворяющих уравнению

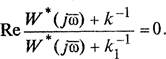                                                                   (2.45)

Для этого подставим в левую часть равенства (2.43) значение (16) = U * (6) + где U (б) — вещественная частотная харакгеристика, И * (б) — мнимая частотная характеристика. Получим

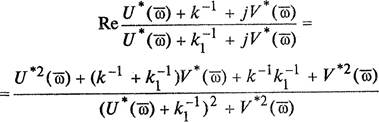 30.

38

Отсюда следует, что

или

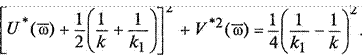2

(2.46)

Уравнение (2.46) представляет собой уравнение окружности с центром в точке 01, имеющей координаты 0 , и раДИУСОМ R = Абсциссы точек пересечения этой окружности с вещественной осью можно определить, полагая у * (б) = 0. Тогда одна точка пересечения имеет абсциссу — 1 Д , а другая точка абсциссу —l/kl. Вне окружности, задаваемой уравнением (2.46) выполняется неравенство (2.43), а внутри этой окружности — неравенство (2.44).

Из изложенного выше следуют критерии абсолютной устойчивости нелинейных дискретных систем, называемые обычно крутовыми.

Состояние равновесия нелинейных дискретных систем с неустойчивой линейной частью, передаточная функция которой содержит т полюсов в правой полуплоскости, и нелинейной характеристикой, принадлежащей сектору (kl, К), будет абсолютно устойчивым, если амплитудно-фазовая частотная характеристика и^д (Д) линейной дискретной части не пересекает окружности (2.46) и охватывает ее против часовой стрелки т/2 раз. Если линейная часть нейтральна, то амплитудно-фазовая частотная характеристика и^х (П) линейной дискретной части не должна пересекать и охватывать окружность (2.46).

В случае, если К1 < 0, для абсолютной устойчивости должно иметь место неравенство (2.44), и критерий формулируется следующим образом: состояние равновесия нелинейных дискретных систем с устойчивой линейной частью и нелинейной характеристикой, принадлежащей сектору (kl, К), где К1 < 0, будет абсолютно устойчивым, если амплитудно-фазовая частотная характеристика и^х Об) расположена внутри окружности. (2.46).

На рис. 28 показан пример абсолютно устойчивой нелинейной дискретной системы, передаточная функция линейной части ко39

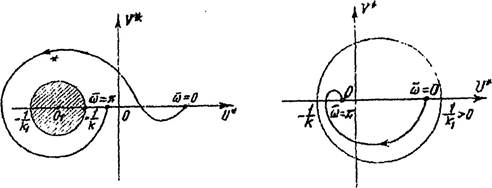
                             Рис. 28                                                         Рис. 29

торой имеет два полюса в правой полуплоскости. Годограф амплитудно-фазовой частотной характеристики (Д) охватывает окружность (2.46) один раз.

На рис. 29 приведен пример абсолютно устойчивой нелинейной дискретной системы с устойчивой линейной частью и нелинейной характеристикой, принадлежащей сектору (kl, К), где Кт < 0. Годограф амшштудно-фазовой частотной характеристики  в этом случае расположен внутри окружности (2.46).

З. МЕТОД ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ В ТЕОРИИ ДИСКРЕТНЫХ СИСТЕМ

Метод гармонической линеаризации широко применяется в инженерной практике при расчете параметров автоколебаний в  непрерывных нелинейных автоматических системах высокого порядка. Это объясняется его относительной простотой и удобством использования в сочетании с хорошо известным аппаратом частотных методов исследования линейных моделей автоматических систем. Применительно к дискретным системам этот метод может быть с успехом использован для анализа периодических процессов.

Систему представляем состоящей из нелинейного импульсного элемента (НИЭ), формирующего элемента (ФЭ) и непрерывной части (НЧ).

40

                                                          ниэ                                                    ПНЧ                                           л[пто1

Рис. ЗО

Формирующий элемент совместно с непрерывной частью образует приведенную непрерывную часть (ПНЧ), НИЭ производит амплитудно-импульсную модуляцию сигнала 6(t) в соответствии с характеристикой Ио), которая полагается симметричной.