Другие предметы \ Теория автоматического регулирования и управления

Теория дискретных систем автоматического управления: Учебное пособие. Часть IV: Нелинейные системы, страница 13

ЛК- ЮбМ

30. ср, ± N). (3.11) 1 —еЛК — r)o м

Если К = 1', то еЛК — r)on = 1, и, следовательно, Коэффициенты

с Е Јлп (3.12)

11=0

Таким образом, Итак, разложение симметричной функции и(п) в ряд (3.7) будет содержать только нечетные гармоники.

(3.9) В этом случае принято обозначать ряд (3.7) со штрихом у знака суммы:

где число л^ксвязано с полупериодом М соотношением (3.6).

и(п) Щ ске

k=-Nl

(3.13)

Совокупность коэффициентов с,. можно назвать комплексным

N, если л^тнечетно,

частотным спектром периодической функции и[п].

где Nl

Рассмотрим, какой вид принимает соотношение (3.9) для сим-	1V — 1, если Л^Ечетно.
метричной периодической функции и(п), для которой М период	Коэффициенты ск этого тригонометрического многочлена вы-
четен и выполняется условие м	ражаются следующим соотношением:

для всех значений п.	Если л^гпри = ^т
В этом случае	нечетно, то К л

—и(п) (3.10) . ПК

2 = СкеЛЈк Q Acos (3.14)

— j1tv (3.15)

Можно заметить, что при N= 1 и N= 2 из (3.13) следует, что функция и[п] будет не только периодической, но и гармоничем ской.

-1

Действительно, при л^т=

+ = С1 COS ЛП,

так как = ё_1 для = 2

Отсюда следует, что коэффициенты ср соответствующие чет- 1 ным индексам r, равны нулю, а коэффициенты, соответствующие

и[п] = —

2 нечетным индексам, определяются формулой

cos —11 + ,

так как ё1 =qe ^NlAcos — + 9 е

При л^т2 З функция u[nl будет в общем случае негармонической. Однако ограничиваясь в (3.13) первой гармоникой, ее можно приближенно представить в виде

^u[ⁿl ^z- ё_те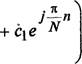= Cl COS —n -FY1 , (3.16)

где, согласно (З. 14),

kSQ[Acos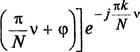 (3.17)

Таким образом, уравнение нелинейного элемента относительно дискретных функций его входа — выхода с учетом (3.16) при-

ближенно может быть получено в форме

И[П] = Cl COS + (Р + D(A, (Р, N) (3.18)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Скачать файл