![]() [п] = е хп cosnn
[п] = е хп cosnn ![]() , Z2[n] =С2е тп cosnn, где т = lnlrl. Исключив из этих равенств время п, получим
уравнение фазовых кривых
, Z2[n] =С2е тп cosnn, где т = lnlrl. Исключив из этих равенств время п, получим
уравнение фазовых кривых
(2 = С-2 COS 7tr![]() expcr
expcr![]()
Если Н <1, то lim Ч [п] = lim [п] = 0.
00 П ОО
![]()
Состояние равновесия называется устойчивым вырожденным узлом
2-го типа.
Если Д > 1, то состояние равновесия представляет собой неустоЙЧИВЫЙ вырожденный узел 2-го типа. Фазовые траектории для устойчивого и неустойчивого вырожденных узлов 2-го типа показаны на рис. 19.
Пример. Построим фазовый портрет дискретной системы, структурная схема которой изображена на рис. 20. Передаточная функция разомкнутой системы
![]()
где d = е-P р = Т[71, Т — период квантования, 7'l — постоянная времени непрерывной части. Тогда передаточная функция замкнугой системы
![]()
19
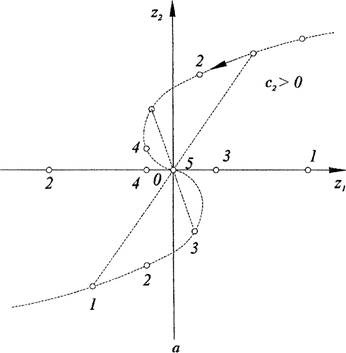
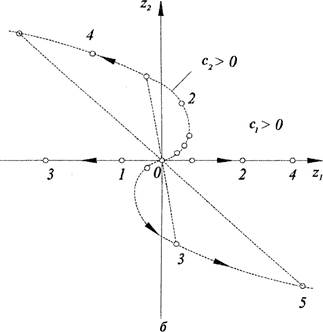
Рис. 18 Рис. 19
20
21
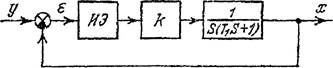
Рис. 20
Разностное уравнение замкнутой системы имеет вид + 2] + +
[К (1 — ф — 1— + 1] + dx[n] = g[nl. Характеристическое уравнение будет r 2
+ [К(1 — ф —1 — dlr + d 0. Для устойчивости системы требуется выполнение
неравенства 0 < К к:![]() Кри-
Кри-
20 + ф тическое значение коэффициента
усиления к кр — —— при значениях параметров системы Т = 1 с, 7'l = 0,25 с будет Ккр =
2,0733. Построим фазовый портрет системы при К = 1. Корни характеристического
уравнения 11,2 = 0,018 ± ј0,133 и у = lrl = 0,1343 <1. Состояние равновесия
представляет собой устойчивый фокус. Фазовые траектории изображены на рис. 21.
Теперь построим фазовый портрет при К = 4 > Ккр. Для этого значения
коэффициента усиления корни характеристического уравнения r1 - -2,9083, ![]() =
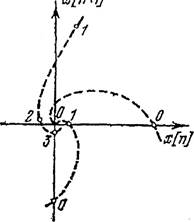
—0,0062. Состояние равновесия представляет собой седло 2-го типа
(седло-розетка). Фазовые траектории приведены на рис. 22.
=
—0,0062. Состояние равновесия представляет собой седло 2-го типа
(седло-розетка). Фазовые траектории приведены на рис. 22.
 477+1]
477+1] 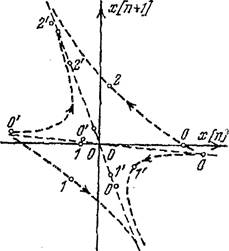
![]() Рис. 21 Рис.
22
Рис. 21 Рис.
22
22
2. АНАЛИЗ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ ДИСКРЕТНЫХ СИСТЕМ
2.1. Основные понятия и определения
Пусть дискретная система описывается системой разностных уравнений
![]() [П + 1] = fi(X1 [П]
[П + 1] = fi(X1 [П]![]() К). (2.1)
К). (2.1)
Правые части уравнений (2.1) полагаются однозначными,
непрерывными функциями переменных п, М, х . Тогда для любых заданных
начальных условий ![]() ш,
..., = хко (2.2)
ш,
..., = хко (2.2)
существует и притом единственное решение системы уравнений (2.1), удовлетворяющее этим начальным условиям. Систему уравнений (2.1) можно записать в векторной форме где х[п]
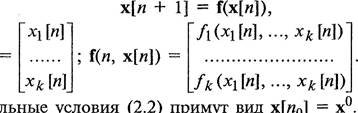 Начальные условия (2.2) примут вид х[по] = х
Начальные условия (2.2) примут вид х[по] = х
Введем определения. Пусть
![]() (2.3)
(2.3)
является некоторым решением системы (2.1), удовлетворяющим начальным условиям е [по] = хо (2.4)
Решение (2.3) называется устойчивым по Ляпунову, если для любого Е > 0 существует такое число б зависящее от Е, что для любого другого решения х = Ап], удовлетворяющего в начальный момент времени п неравенству е [по] — р < 5, будет справедливо неравенство [п] — р < е для всех п по .
Решение (2.3) называется неустойчивым по Ляпунову, если существует такое число Е > 0, что для любого числа б > О найдется такой момент времени > по, что будет справедливо неравенство ll [111] — р [щ Е, несмотря на то, что имело место неравенство
Решение (2.3) называется асимптотически устойчивым, если: 1) это решение устойчиво; 2) существует такое число А 0, что для
23
любого решения х = р [п], удовлетворяющего при п по
неравенству ll [по] — <А, будет справедливо lim [п] — р [п]![]()
П 00
Движение, соответствующее решению х = е [п], обычно называют невозмущенным Движением. Другие решения х = p[nl, которые могут быть получены при изменении начальных условий, соответствуют возмущенным движениям. С помощью замены переменных
![]() (2.5)
(2.5)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.