Теория дискретных систем автоматического управления: Учебное пособие. Часть IV: Нелинейные системы, страница 3

+4

85

62

4

                            Рис. З                                                               Рис. 4

8

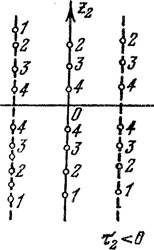
Случай 2. Числа rl и различны и отрицательны, причем t2l > ht. Запишем решение (1.18) в виде

                                       (1.22)

                              —                етап где Ч = lnhl, =lnt2l. Если п четное, то q[nl = , Z2[ⁿl = С2е^ПТ2 . Отсюда следует, что фазовые траектории при четных значениях п совпадают с траекториями для положительных значений  и при соответствующих значениях Ч и . Для нечетных значений п имеем [п] = , ф [п] = -С2е ^Т2П Сравнивая формулы (1.21) и (1.22), найдем, что для нечетных значений п фазовые траектории располагаются на непрерывных кривых, симметричных относительно начала координат кривым для фазовых траекторий при положительных значениях и П, соответствующих значениям Ч и т2. Получим уравнение фазовых кривых. Для этого запишем решение (1.22) в виде

Zl [П] = Z1 [01cos пп е ЧП Z2 [п] = Z2 [0] COS пп е ЧП

                =                                             1         Zl[nlz2Pl

где Ч [^О ]                      ^Z2[⁰ 1 - ст Тогда п =     ln

Уравнение фазовых кривых будет

. (1.23)

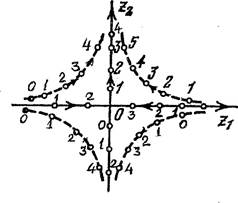
Если числа rl и удовлетворяют условию 1 r1 > П, то состояние равновесия представляет собой устойчивый узел 2-го типа (розетка-узел). Фазовые траектории и фазовые кривые для этого состояния равновесия показаны на рис. 5.

Если имеют место неравенства > > 1, то состояние равновесия представляет собой неустойчивый узел 2-го типа.

Пусть теперь hl <1, > 1. Тогда Ч <0, а >O. Состояние равновесия называется се лом 2-го типа (розетка-сеДло) . Характер фазовых траекторий и фазовых кривых указан на рис. 60

Если одно из чисел (1⁴1 или ф) равно —1, например r1 = —1, то общее решение имеет вид [п] = (—1)^п , ф [п] = е ^тјп и фазовые траектории представляют собой последовательности точек на прямых, параллельных оси ф. Эти последовательности сходят9

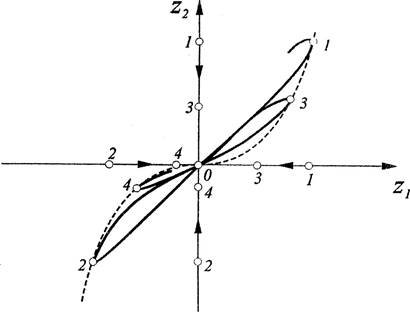
Рис. 5

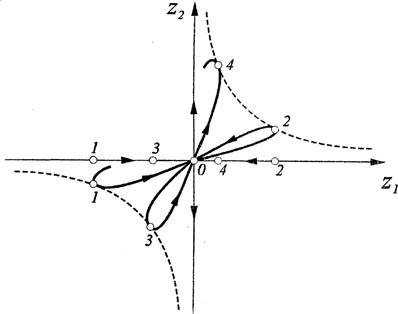
Рис. 6

ся к оси при и расходятся при >0. На рис. 7 изображены фазовые траектории при <0, представляющие собой две последовательности точек, первая из которых по прямой q = сверху и вторая по прямой = —Cl снизу стремятся к оси Ч.

10

Рис. 7

Случай 3. Пусть числа и имеют разные знаки, например  > 0, а < 0. Тогда решения (1.18) можно записать так:     

                              ^Z l =(1 Р] е 11/1                         1.24)

 — Z2 [0] COS е т 211

где                  =Cl, Z2[01 =с2•, =lnrl,

При четных значениях п уравнения фазовых траекторий совпадут с уравнениями (1.20), а для нечетных значений п примут вид

                                                          ^Z 2 = —С2е                                                         (1.25)

Сравнивая формулы (1.20) и (1.25), найдем, что для нечетных значений п фазовые траектории располагаются на непрерывных кривых, симметричных относительно оси кривым для фазовых траекторий при положительных значениях и П, соответствующих значениям тт и . Уравнение фазовых кривых будет

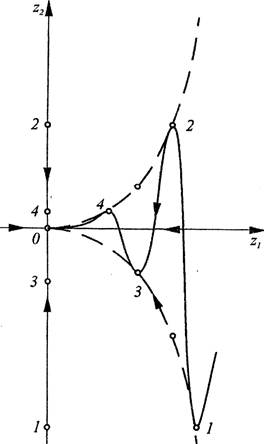
Z2[nl = Z2[Ol cos [л1/ч ln(Zi [n]/Zl         [111/Z1              (1.26) Если числа и удовлетворяют условию < 1, t2l <1, то состояние равновесия представляет собой устойчивый узел 3-го типа (устойчивая змейка). Фазовые траектории и фазовые кривые для этого состояния равновесия показаны на рис. 8. Если имеют место неравенства > 1, Д > 1, то состояние равновесия представляет собой неустойчивыи узел 3-го типа (неустойчивая змейка). Фазовые траектории и фазовые кривые для этого состояния равновесия показаны на рис. 9. Пусть теперь либо rl < 1, > 1, либо > 1, t21 < l. Состояние равновесия называется сетом 3-го типа (прямой конус, если > 1, и обратный конус, если > 1). Характер фазовых траекторий и фа-

30вых кривьж указан на рис. 10 и 11.

2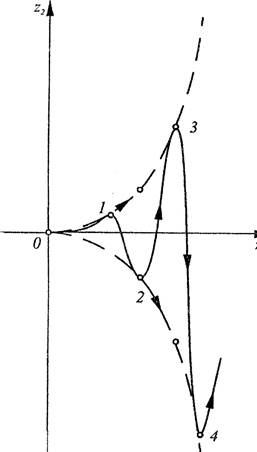

                            Рис. 8                                                          Рис. 9

12

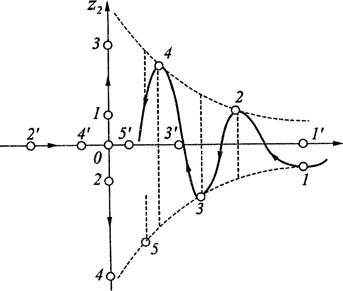
Рис. 10