Другие предметы \ Теория автоматического регулирования и управления

Теория дискретных систем автоматического управления: Учебное пособие. Часть IV: Нелинейные системы, страница 2

Для упрощения исследования приведем матрицу А к жордановой форме с помощью некоторого линейного невырожденного преобразования с матрицей Т:

(1.9)

Тогда система уравнений (1.8) примет вид rr1ATz[nl,     (1.10)

причем т—1АТ = Ј — жорданова форма матрицы А. Обозначим и i2 корни характеристического уравнения det(A -- ЖЕ) = О. (1.11)

Если эти корни различны, т. е. М 12 , то система уравнений (1.10) в скалярной форме имеет вид

                                                                         (1.12)

или

                                                                      (1.13)

5

где = + 1, = i2 + 1 представляют собой характеристические числа матрицы В = А + Е.

Если корни характеристического уравнения (1.11) кратные, т. е. i1 = i2 до жорданова форма матрицы А будет либо .Ј либо .Ј —

В первом случае система уравнений (1.10) примет вид

во втором —

[п] + Z2[nl,

(1.15)

Системы уравнений (1.14) и (1.15) запишем соответственно

                                                                      (1.16)

и

                                                           (1.17)

причем = il + 1.

Общее решение системы разностных уравнений (1.13) будет выглядеть так:

                  Z l [П] = сип                 nlnrl П = С2еnlnr2           (1.18)

где и c2 — произвольные постоянные.

Аналогичный вид имеет общее решение системы уравнений

 (1.16), необходимо только положить r1 п = слеnlnrl.п = спеnlnrl (1.19) = си

Общее решение системы уравнений (1.17) запишем следующим образом:

+ C2nr{i 1 '(1.20)

nlnrl

6

Если заменить в равенствах (1.18) — (1.20) дискретное время п на непрерывное t, то этим равенствам на фазовой плоскости будут соответствовать непрерывные кривые, которые представляют собой фазовые траектории системы линейных дифференциальных уравнений второго порядка с характеристическими числами ln и ln 142, если эти числа вещественны. В дальнейшем это обстоятельство будет широко использоваться. Фазовые траектории системы линейных дифференциальных уравнений второго порядка для различных типов состояний равновесия подробно рассмотрены в

Если исключить в равенствах (1.18) — (1.20) дискретное время п, то полученное равенство Z2[nl = f(Cl, ф, Zl[nl) представляет собой уравнение фазовой кривой.

Рассмотрим пять различных случаев построения фазовых траекторий.

Случай 1. Пусть числа и различны и положительны. Обозначим Ч = lnn и = lnn . Тогда общее решение (1.18) примет вид

                                                      (1.21)

Уравнение фазовой кривой будет

Т2/ч

ст 2/Х1

Возможны следующие типы состояний равновесия.

Если числа и r2 удовлетворяют условию 1 > > r2 > О, то В соответствии с формулами (1.21) получим lim [п] = lim ф [п]

П 00

Состояние равновесия представляет собой устойчивый узел 1-го типа. Фазовые траектории для этого состояния равновесия покаиНЫ на рис. 1. Так как > 0, то фазовые кривые представляют собой кривые параболического типа.

Пусть теперь r2 > > 1. Тогда lim Zl[nl =lim Z2[nl = 00.

                                                                                                     П 00

Состояние равновесия представляет собой неустойчивый узел 1-го типа. Фазовые траектории для этого состояния равновесия показаны на рис. 2. Фазовые кривые и в этом случае будут кривыми параболического типа.

          Если имеют место неравенства > Л, > 1, то Ч             т2

7

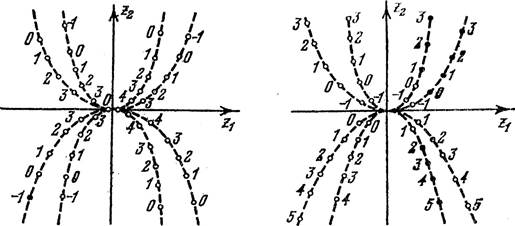
                           Рис.                                                                Рис. 2

Тогда lim                    lim Z2[nl = т. Так как  то фазовые

П - » оо кривые представляют собой кривые гиперболического типа. Состояние равновесия называется сеДлом Его ,ТшШ- Фазовые траектории для этого состояния равновесия изображены на рис. З.

Если одно из чисел (П или равно единице, например - 1, то общее решение имеет вид ч [п] — — с2 еТ2П и фазовые траектории представляют собой последовательности точек на прямых, параллельных оси ф. Эти последовательности сходятся к оси при и расходятся при На рис. 4 изображены фазовые траектории при <O.

Скачать файл