Теория дискретных систем автоматического управления: Учебное пособие. Часть IV: Нелинейные системы, страница 14

где D(A, ЛО = (А, N) — (Р.

Переходя теперь в (3.18) и в (3.2) к Фурье-изображениям, можно записать

где

                                   (3.19)

дискретный коэффициент гармонической линеаризации нелинейного элемента Их). Рассмотрим основные свойства коэффициента     (Р, ЛЭ.

Прежде всего следует заметить, что в отличие от непрерывных систем коэффициент и^х (А, (Р, ЛО даже для однозначных симметричных нелинейных характеристик является функцией не только от амплитуды, но таюке от частоты (или полупериода ЛО и фазы (Р периодического режима.

46

Кроме того, коэффициент и^и (А, ф, N) есть периодическая по

(Р функция с периодом

Q Acos 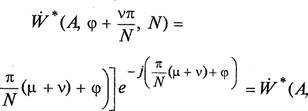 (Р, ЛЭ.

Отсюда следует, что при построении дискретного коэффициента гармонической линеаризации достаточно ограничиваться рассмотрением фаз, лежащих в пределах одного периода длины

 например в диапазоне от —

      Из выражения (3.19) следует, что коэффициент            ф, N)

симметричен относительно оси абсцисс при противоположных по знаку значениях фазы (Р из указанного диапазона, т. е.

х Acos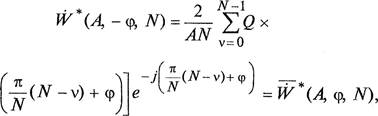

где черта сверху означает комплексно-сопряженную величину.

3.2. Определение параметров периодических решений

Рассмотрим определение параметров автоколебаний методом гармонической линеаризации.

47

Предположим, что в нелинейной импульсной системе (см. рис. 30) имеет место периодический режим полупериода N. Тогда уравнения системы могут быть записаны в следующем виде:

*

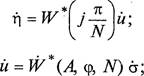
где РК                — импульсная частотная характеристика и^х (Д) приведенной линейной части системы на частоте о —

Исключая из этих уравнений переменные й и Й, получаем

+1 6=0.

Это уравнение будет удовлетворяться при условии

                                                     (3.20)

Соотношение (3.20) является характеристическим уравнением гармонически линеаризованной системы и служит основой для определения параметров периодических режимов; его можно представить в виде

                                                          (3.21)

Для определения амплитуды А и фазы ф периодического режима нужно на комплексной плоскости построить частотную характеристику и^д (16) и изобразить семейство кривых —

соответствующих обратной величине дискретного коэффициента гармонической линеаризации, взятого с обратным знаком. Если одна из кривых этого семейства проходит через точку с отметкой — частотной характеристики W Об), то периодический режим полупериода л^т существует. Его фаза определяется значением параметра (Р этой кривой семейства, а амплитуда А — оцифровкой  этой кривой (рис. 31).

Вычислим дискретный коэффициент гармонической линеаризации для релейной характеристики (рис. 32).

при N 2 —— S тогда

                              4         

                — —[Q(A 1 cosq)) +                 —

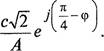
При определении автоколебаний для N= 2 нужно построить графиш:

48

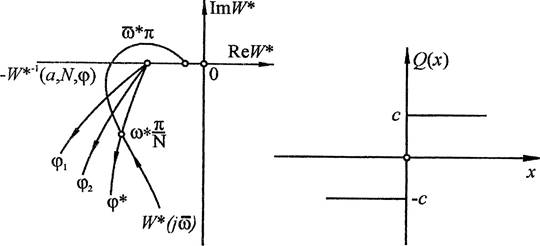
                              Рис. 31                                                        Рис. 32

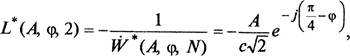
семейство прямых линий, расположенных внутри угла S — (рис. 33).

4 при = З

                         =                   [Q(A cos (Р) + А Si (Р +            Х

ЗА6

                  6 +0 Асо   

следовательно, при О (Р S

6

ЗА

Соответствующие графики L*(A, (Р, З) расположены в секторе

5п          Зл

6             6

49

2

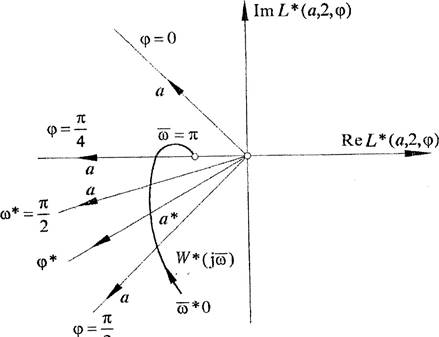
Рис. 33

при л^т 4

8 ул

      Прямые            ф, 4) лежат в секторе

88

На рис. 33 показан годограф  соответствующий условиям возникновения автоколебаний при л^к = 2. Фаза автоколебаний (Р определяется прямой, проходящей через точку И⁷ ј—   2

Условие возникновения автоколебаний имеет вид

                                    Зл                 * л 5л

                              —sargPV         S

                                     4                            4

Для исследования устойчивости автоколебаний справедливы те же критерии, что и в случае непрерывных систем. Так, если годограф (Д (Р, ЛО при увеличении А выходит из области, ограниченной годографом и^х (Д), то автоколебания устойчивы.

50

Рассмотрим еще один пример. Пусть амплитудно-фазовая частотная характеристика непрерывной части системы имеет вид Кор