Структура систем массового обслуживания. Входной поток заявок. Приборы (каналы) обслуживания. Показатели эффективности СМО, страница 9

P₀(t_пер) = P_0уст – P_0уст e ^{– (λ+µ)tпер} , где t_пер – длительность переходного процесса.

Рисунок 16

Следовательно,

.

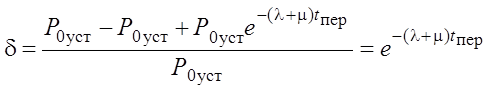Отсюда:      .

Пример.             λ = 0,1 заявки/мин, µ = 0,2  заявки/мин,

.

При  δ = 0,01 = 1%   –  

При δ = 0,05 = 5%    –  

Вывод: Если длительность работы системы большая (часы или дни), то нестационарный режим можно не учитывать.

Замечание. Аналогичные исследования других систем массового обслуживания показывают, что переходной режим продолжается , где  – средняя длительность обслуживания.

2.1.2. Стационарный режим

Условие существования стационарного режима для одноканальной системы: , если >1, то стационарного режима нет (прибор не успевает обслуживать заявки); для n–канальной системы: , если , то приборы не успевают обслуживать заявки.

Рассматриваемая система имеет два состояния S₀ и S₁ и переходит из одного состояния в другое с интенсивностями λ и µ (рис. 17).

СостояниеS₀  – обслуживающий прибор свободен;

Состояние S₁  – обслуживающий прибор занят.

Рассматриваем стационарный режим, при котором вероятности состояний не зависят от времени: при t производные  = 0.

Требуется найти P₀  и P_1.

 Рисунок 17

Составим систему алгебраических уравнений (уравнения составляются так же, как дифференциальные уравнения, только здесь производные равны 0)

– λ P₀ + µ P₁ = 0,                                                                                 (1)

λ P₀ – µ P₁ = 0,

P₀ + P₁ = 1.                                                                                       (2)

Из (1) получаем .

Подставив P₁  в (2), получаем             .

Откуда 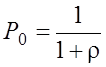.              .                                                                   (2^’)

С учетом (2')     .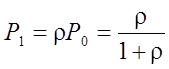    

Параметры системы

§  λ – интенсивность поступления заявок;

§  µ – интенсивность обслуживания (µ = 1/t, где t – средняя длительность обслуживания заявки);

§  ρ = λ/µ – загрузка системы          (µ<>0 ),       0≤ ρ ≤1;

ρ = 1 – полная загрузка;   ρ = 0 – система свободна;

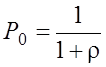§    = q = 1 – P₁  – относительная пропускная способность – доля обслуженных заявок;

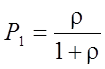§   – вероятность отказа (прибор занят);

§  А = λq – абсолютная пропускная способность – среднее число обслуженных заявок в единицу времени.

2.2. Система с очередью

Рассмотрим систему М/М/1/1 – это одноканальная система с одноместной очередью, поток заявок и обслуживание экспоненциальные.

Структурная схема системы показана на рис. 18.

Временная диаграмма работы системы показана на рис. 19.

На этой временной диаграмме, по сравнению с рис. 14, добавлена временная ось очереди, на которой показаны интервалы времени  пребывания заявок в очереди.

 Рисунок 18

 Рисунок 19

Эта система имеет уже три состояния:

S₀ – система свободна (прибор не занят, очередь пуста);

S₁ – прибор занят, очередь пуста;

S₂ – система занята (прибор и очередь заняты).

Граф переходов системы из состояния в состояние показан на рис. 20.

Рисунок 20

Система уравнений:

– λ P₀ + µ P₁=0;                                                                                                                    (1)

λ P₀ – (λ+µ) P₁ +µ P₂=0;                                                                                                       (2)

λ P₁ – µ P₂=0;                                                                                                                       (3)

P₀ + P₁+ P₂ =1.                                                                                    (4)

Из (1)   .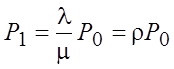

Из (3)    .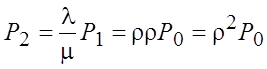

Из (4)  .

Откуда

P₀ = 1/(1+ ρ + ρ²) = (1– ρ)/(1– ρ³), так как 1+ ρ + ρ² = (1– ρ³)/(1– ρ)  – как сумма членов геометрической прогрессии, первый член которой b₁=1, знаменатель q = ρ.

ПРИМЕЧАНИЕ:Для геометрической прогрессии сумма n членов равна:

S_n= b₁(1–qⁿ)/(1–q), где b₁ – первый член, q<>1 – знаменатель.

Теперь рассмотрим систему с очередью длины m – систему М/М/1/m.