Структура систем массового обслуживания. Входной поток заявок. Приборы (каналы) обслуживания. Показатели эффективности СМО, страница 7

Для контроля получаемых результатов удобно пользоваться функциональными связями параметров системы:

n₀ + n_з = n,

 = ,

= ,

 = _o+_п, где            _o = A – интенсивность обслуженных заявок,

_п – интенсивность потерянных заявок.

При оценке эффективности СМО могут быть использованы также стоимостные показатели:

q_обс – стоимость обслуживания заявки в системе;

q_ож – стоимость потерь, связанная с простоем заявки в очереди;

q_у – стоимость убытков из–за потери заявки;

q_k – стоимость эксплуатации k–го прибора в единицу времени;

q_пk – стоимость единицы времени простоя k–го прибора;

c –экономический эффект, получаемый при обслуживании заявки.

При выборе оптимальных параметров СМО по экономическим показателям можно использовать функции потерь:

– для систем с ожиданием

С_п = (q_ож+q_пkn₀ + q_kn_з)T,    где T – интервал времени;

– для систем с отказами

С_п = (q_уp_n + q_kn_з)T;

– для смешанных систем

С_п = (q_ож+q_пkn₀ + q_уp_n+ q_kn_з)T.

Оценку экономической эффективности системы можно производить по выражению

E = AcT – С_п .

Другие параметры будут представлены при рассмотрении соответствующих систем.

При исследовании и определении оптимального варианта обычно в качестве переменных выбирают параметры , , n, некоторую дисциплину обслуживания и структуру системы.

2. Одноканальные системы массового обслуживания

2.1. Система с отказами

Рассмотрим систему М/М/1/0 – это одноканальная система с отказами, поток заявок и обслуживание экспоненциальные.

Структурная схема системы показана на рис. 13.

Работа системы ясна из ее временной диаграммы, показанной на рис. 14.

На рис. 14 поток заявок представлен в виде точек на оси времени, появляющихся через случайные интервалы времени t_i , обслуживание заявок представлено интервалами времени t_i на своей оси времени, потери заявок – точки, имитирующие заявки, попавшие на интервалы обслуживания других заявок.

Рисунок 13

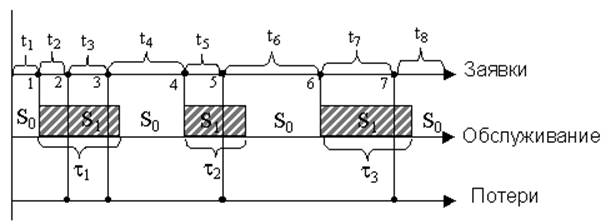
 Рисунок 14

Для любой системы массового обслуживания можно выделить два периода ее работы: нестационарный и стационарный.

2.1.1. Нестационарный режим

Рассмотрим нестационарный режим работы нашей системы (М/М/1/0).

Система может находиться в одном из двух состояний:

-  обслуживающий прибор свободен – S₀;

-  обслуживающий прибор занят – S₁.

Обозначим

P₀(t) – вероятность нахождения системы в состоянии S₀;

P₁(t) – вероятность нахождения системы в состоянии S₁.

Для этих вероятностей справедливо 

P₀(t) + P₁(t) = 1.

Попытаемся получить уравнения, описывающие поведение вероятностей P₀(t) и P₁(t) во времени.

Возможные переходы системы из состояния в состояние представим в виде графа переходов рис. 15, а.

Рисунок 15

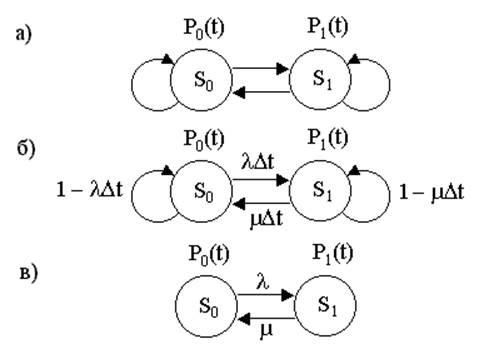Фиксируем момент t и найдем вероятность P₀(t+∆t) того, что система будет находиться в S₀  через интервал времени ∆t. Это может произойти двумя способами:

А – система находилась в S₀  и не перешла в S₁ (не было ни одной заявки). Это событие на графе представлено петлей при состоянии S₀.

В – система находилась в S₁, и за ∆t обслуживание заявки закончилось и система перешла в S₀. Это событие показано на графе дугой из состояния S₁ в состояние S₀.

Возможностью перескока S₀ – S₁ – S₀ пренебрегаем – поток ординарен (вероятность двух событий за ∆t ничтожно мала).

По теореме сложения вероятностей

P₀(t+∆t) = Р(А)+Р(В).

Найдем Р(А).

В момент времени t вероятность нахождения системы в состоянии S₀ равна P₀(t). Вероятность того, что за ∆t не придет ни одной заявки, т.е. того, что система останется в состоянии S₀, равна e^–λ∆t. (Это следует из закона пуассона; при k = 0 получаем  p₀(∆t) = e^–λ∆t .)

При   λ∆t <<1 можно положить       e^–λ∆t ≈ 1– λ∆t.

Эта вероятность показана на графе рис. 15,б у петли при состоянии S₀.

По теореме умножения вероятностей находим

Р(А) = P₀(t)(1– λ∆t).

Это вероятность того, что система находилась в S₀ и осталась в этом состоянии, так как не было заявок.

Найдем Р(В).

Вероятность того, что система находилась в S₁, равна P₁(t).