– ординарностью;
– отсутствием последействия.
- Поток стационарен, если вероятность попадания k событий на любой участок зависит только от его длительности, но не от его положения на оси времени.
-
Поток ординарен, если вероятность попадания двух и
более событий на элементарный участок ![]() несоизмеримо
меньше вероятности появления одного события.
несоизмеримо
меньше вероятности появления одного события.
- Поток без последействия, если вероятности появления событий для любых непересекающихся интервалов времени не зависят друг от друга.
Из теории известно, что сумма большого числа (>3) случайных потоков (без преобладания) с произвольными законами распределения асимптотически сходится к пуассоновскому потоку (см. рис. 12, а).
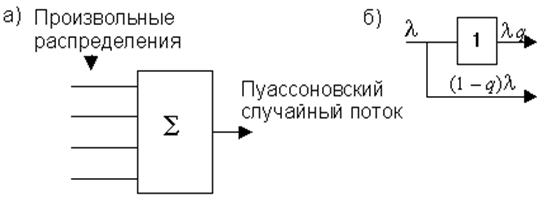 |
Другим действием, часто выполняемым над потоками, является просеивание. Просеивание применительно к пуассоновскому потоку определяется следующим образом.
Пусть имеется пуассоновский поток с
интенсивностью ![]() , а
операция просеивания задается так, что с вероятностью q очередное событие остается в потоке и с вероятностью 1 – q удаляется из потока. Результирующие потоки будут пуассоновскими с
интенсивностями
, а
операция просеивания задается так, что с вероятностью q очередное событие остается в потоке и с вероятностью 1 – q удаляется из потока. Результирующие потоки будут пуассоновскими с
интенсивностями ![]() q и (1 – q)
q и (1 – q)![]() соответственно (рис. 12,б).
соответственно (рис. 12,б).
8. По закону обслуживания заявок:
– Экспоненциальный (считается, что это самый тяжелый случай)
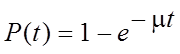 – вероятность
завершения обслуживания за время t,
– вероятность
завершения обслуживания за время t, ![]() – интенсивность
обслуживания заявок.
– интенсивность
обслуживания заявок. ![]() = 1/
= 1/![]() , где
, где ![]() – среднее
время обслуживания заявок.
– среднее
время обслуживания заявок.
– Равномерный.
– Произвольный.
– Смещенный экспоненциальный – всегда есть некоторое время на прием заявки.
–
Регулярное обслуживание (![]() const).
const).
9. По наличию взаимопомощи:
– без помощи – заявки обслуживает один прибор с интенсивностью µ;
– работают n параллельных приборов – их интенсивность nµ.
СМО можно задать не схемой, а перечислением свойств, например, так
X1/X2/X3/X4/X5,
X1 – характеристика входного потока заявок;
X2 – характеристика обслуживания заявок;
X3 – количество каналов обслуживания (1…n);
X4 – длина очереди (0, m, ∞), m – длина очереди;
X5 = 0 – без приоритетов;
1 – относительный приоритет;
2 – абсолютный приоритет.
В качестве характеристик входного потока и обслуживания заявок задают законы распределения в виде условных обозначений:
M – экспоненциальный закон;
D – регулярное поступление заявок;
Еk – k–й закон Эрланга;
G – произвольный закон.
Пример. Система М/М/1/0 – одноканальная система с потерями с экспоненциальным законом поступления заявок и экспоненциальным законом обслуживания.
Эффективность СМО можно характеризовать большим числом различных показателей. К числу наиболее часто применяемых показателей относятся следующие показатели:
§ вероятность потери заявки pотк, для систем с потерями она равна вероятности занятости всех обслуживающих приборов pn;
§ относительная пропускная способность системы q = 1 – pотк – доля обслуженных заявок;
§
абсолютная пропускная способность системы A = ![]() q – интенсивность заявок, обслуженных системой;
q – интенсивность заявок, обслуженных системой;
§ вероятность того, что обслуживанием занято k приборов – pk, частным случаем этого показателя являются pn – вероятность занятости всех приборов и p0 – вероятность того, что все приборы свободны;
§
среднее число занятых приборов nз
= ![]() =
= 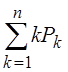 ;
;
§
среднее число свободных приборов n0 = 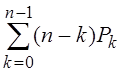 ;
;
§ коэффициент простоя приборов Kп = n0/n;
§ коэффициент занятости приборов Kз = nз/n;
§
средняя длина очереди ![]() =
= 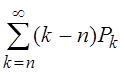 ,
(
,
(![]() =
= 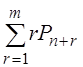 );
);
§
среднее время ожидания в очереди ![]() =
= ![]() /
/![]() ;
;
§
среднее число заявок, находящихся в системе ![]() ;
;
§
средняя длительность обслуживания заявки ![]() ;
;
§
среднее время пребывания заявки в системе ![]() =
=
![]() +
+ ![]() ;
;
§
вероятность того, что число заявок в очереди больше
некоторого числа m Pr>m = 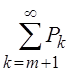 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.