Структура систем массового обслуживания. Входной поток заявок. Приборы (каналы) обслуживания. Показатели эффективности СМО, страница 15

Время выполнения операции каждым прибором является величиной случайной, подчиняющейся показательному закону с параметрами  и  соответственно для первого и второго приборов. На первый прибор поступает простейший поток заявок с интенсивностью  заявок в единицу времени. Заявки, которые не были обслужены первым прибором из–за его занятости, поступают на второй прибор. Если он свободен, то заявки обслуживаются им, в противном случае заявки считаются потерянными.

Рисунок 36

Обозначим состояния системы:

S₀₀ – первый и второй приборы свободны от обслуживания;

S₁₀ – первый прибор занят обслуживанием, второй свободен;

S₀₁ – первый прибор свободен, второй занят обслуживанием;

S₁₁ – оба прибора заняты обслуживанием.

Граф переходов системы показан на рис. 37.

В стационарном режиме система описывается следующими уравнениями

Рисунок 37

Решение этой системы уравнений дает следующие результаты:

§  Вероятность того, что все приборы свободны от обслуживания

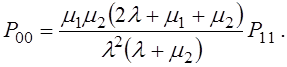
§  Вероятность того, что занят обслуживанием только первый прибор

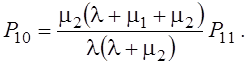
§  Вероятность того, что занят обслуживанием только второй прибор

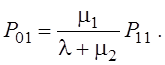
§  Вероятность отказа в обслуживании заявки, которая равна вероятности того, что заняты оба прибора

                  (1)

Зная вероятности состояний системы, можно определить загрузку каждого прибора. Определим коэффициенты загрузки приборов как отношение математического ожидания числа заявок, обслуженных прибором в единицу времени, к математическому ожиданию числа заявок, обслуженных обоими приборами в единицу времени.

§  Доля обслуженных заявок

q = .

§  математическое ожидание числа заявок, обслуженных обоими приборами в единицу времени равно

A = .

§  Математическое ожидание числа заявок, обслуженных первым прибором в единицу времени, равно , для второго прибора оно равно .

§  коэффициент загрузки первого прибора равен

K₃₁ =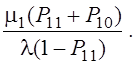

§  коэффициент загрузки второго прибора равен

K₃₂ =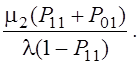

После подстановки значений Р₁₁, Р₁₀ и Р₀₁ получим

K₃₁ =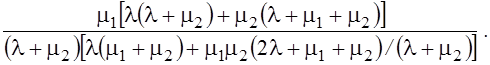

K₃₂ =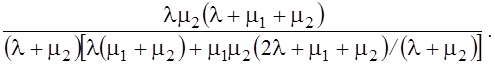

§  Отношение

R₁₂ = K₃₁/ K₃₂ =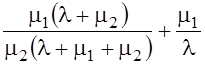

показывает, во сколько раз один прибор работает больше, чем другой.

Анализ уравнения (1) показывает, что для наибольшей эффективности системы, первый прибор должен иметь высшую производительность. Например, при создании контрольного пункта из двух стендов разной производительности первым следует ставить стенд, который имеет большую производительность. В этом случае на второй прибор пойдет более редкий поток заявок. Для обслуживания этого потока можно использовать прибор меньшей производительности.

3.4. Система с очередью

Структурная схема системы с очередью M/М/n/mпоказана на рис. 38.

Граф переходов системы показан на рис. 39.

Здесь, начиная с S_n, все , так как работают все n приборов,  для i = 0, 1, 2,…, (n+m–1).

Условие существования стационарного режима, т.е. когда P₀, P₁,…, P_n+m имеют конечные значения:     .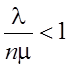

Если 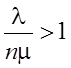  , то очередь будет неограниченно расти.

 Рисунок 38

Рисунок 39

Система уравнений здесь будет такой

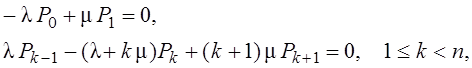
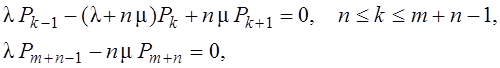
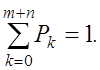
где     n – количество приборов, m – количество мест в очереди.

Граф системы представляет собой типичную схему «гибели и размножения», для которой решение в общем виде уже получено

P_i= α_i P₀,    

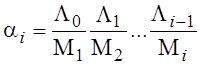 ;    α₀=1.

_.    

 _.

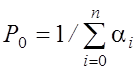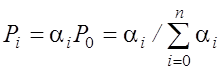Подставив значения  и  и произведя замену 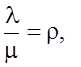получаем

; 

;

…

;

…

;

;

;

…

.

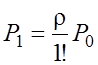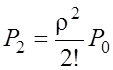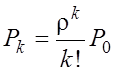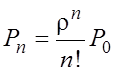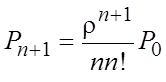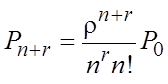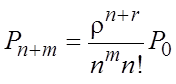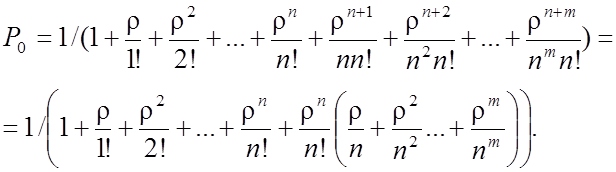
Сумма 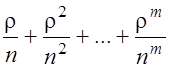 представляет собой сумму геометрической прогрессии с первым членом и знаменателем, равными , поэтому

Параметры системы

§  Вероятность того, что все приборы свободны

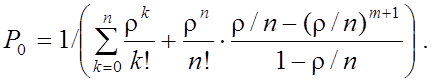
§  Вероятность того, что все приборы заняты

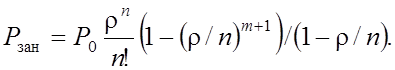
§  Вероятность отказа в обслуживании заявки

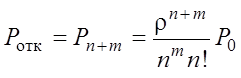 – все n приборов и m мест в очереди заняты.

§  Относительная пропускная способность, т.е. доля обслуженных заявок

q = 1 – P_отк = 1 – .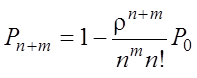

§  Абсолютная пропускная способность