Структура систем массового обслуживания. Входной поток заявок. Приборы (каналы) обслуживания. Показатели эффективности СМО, страница 17

В вычислительных системах к таким «нетерпеливым» заявкам могут относиться заявки с ограниченным срокам годности информации.

Рассматриваемая система представляет собой некоторое множество систем массового обслуживания: задаваясь разными значениями n, m, ,, можно получить одноканальные и многоканальные системы с очередью и без очереди, с потерями и без потерь, с ограниченным и неограниченным временем пребывания заявки в системе. 

Рисунок 44

Пусть все потоки в системе пуассоновские. Найдем для системы вероятности состояний.

Состояния системы

S₀ — все каналы свободны,

S₁ — занят один канал,

…

S_k — заняты k каналов,

…

S_n — заняты все п каналов,

S_n+1 — заняты все п каналов, одна заявка стоит в очереди,

…

S_n+r — заняты все п каналов, r заявок стоят в очереди,

…

S_n+m — заняты все п каналов, m заявок стоят в очереди.

Граф состояний системы показан на рис. 45. Он отличается от графа переходов системы M/М/n/m тем, что интенсивность освобождения занятого канала здесь равна , а также тем, что, начиная с состояния S_n+1, когда начинает образовываться очередь, к интенсивности освобождения всех n каналов добавляется интенсивность уходов заявок из очереди. Если в очереди стоят r заявок, то суммарная интенсивность потока уходов заявок из–за окончания срока годности их информации здесь равна rv, а общая интенсивность уходов заявок из состояния S_n+r системы будет равна n*+ rv.

Как видно из графа, опять имеем схему “гибели и размножения”.

Рисунок 45

применяя общие выражения для предельных вероятностей состояний в этой схеме и произведя замену , получим

; 

…

;

…

;

;

;

…

;

…

_.

…

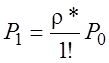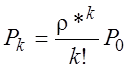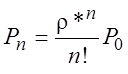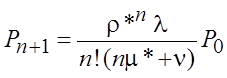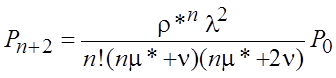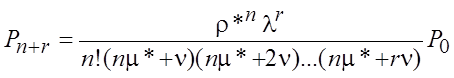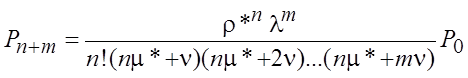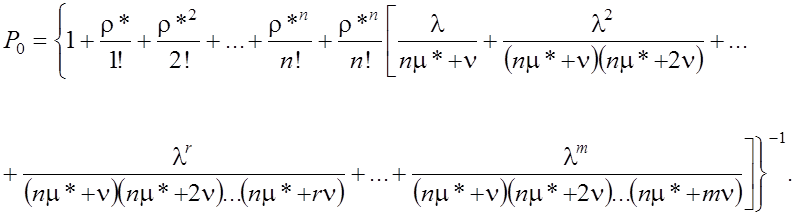
Вводя обозначение , для вероятностей, начиная с P_n+1, получим

;

…

;

…

;

.

Параметры системы

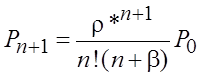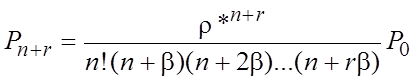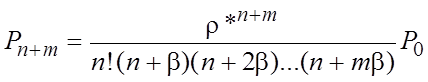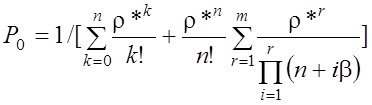§  Интенсивность входного потока – .

§  Интенсивность обслуживания – .

§  Интенсивность уходов заявок из очереди – .

§  Интенсивность уходов заявок из под обслуживания – .

§  Интенсивность освобождения канала –  – канал освобождается либо в связи с завершением обслуживания заявки, либо из–за ухода заявки из системы.

§  Среднее число занятых каналов можно найти как математическое ожидание случайной величины W, принимающей конечное число значений   0, 1, 2, ..., п с вероятностями р₀, P₁,…, P_n–1, 1 – (Р₀+P₁+P₂+…+P_n–1).

Последняя вероятность равна 1 – (Р₀+P₁+P₂+…+P_n–1), так как, начиная с состояния S_n, все n приборов заняты обслуживанием.

Следовательно,   

= 0 =

= .

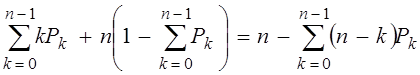§  Абсолютную пропускную способность системы найдем из выражения  

A = .

§  Относительная пропускная способность системы будет равна

P_обс = q = A/=/=/.

§  Вероятность отказа в обслуживании заявки

P_отк = 1 – P_обс.

§  Среднее число заявок в очереди

.

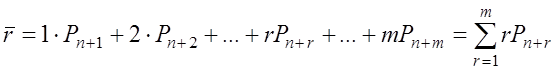§  Вероятность того, что канал (любой) занят

P_зк = /n.

§  Вероятность того, что канал (любой) не занят

P_нк = 1 – P_зк = 1 – /n.

§  Вероятность полной загрузки системы (все n каналов заняты)

P_зс = .

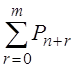§  Среднее время полной загрузки системы

.

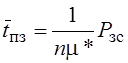§  Среднее время неполной загрузки системы

.

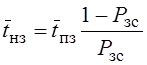§  Вероятность наличия очереди

P_но = .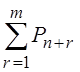

§  Среднее время наличия очереди

.

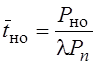§  Среднее время занятости канала

.

§  Среднее время простоя канала

.

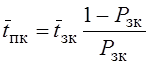§  Среднее время пребывания заявки в очереди

.

§  Среднее время пребывания заявки в системе

.

3.7. Замкнутые системы

3.7.1. Система технического обслуживания

Имеется т одинаковых технических устройств, каждое из которых может в некоторые случайные моменты времени нуждаться в обслуживании (например, из–за отказов). Поток заявок каждого технического устройства пуассоновский с интенсивностью . Техническое устройство в нашем случае – это компьютерные системы или их отдельные устройства. Каждое техническое устройство может обслуживаться одним из п каналов. Интенсивность пуассоновского потока обслуживаний каждого канала . Если к моменту отказа технического устройства все п каналов будут заняты, то оно встанет в очередь на обслуживание. Дисциплина очереди естественная: «кто раньше пришел, тот раньше обслуживается».