Структура систем массового обслуживания. Входной поток заявок. Приборы (каналы) обслуживания. Показатели эффективности СМО, страница 12

Рисунок 24

Фрагмент графа переходов системы показан на рис. 25.

Рисунок 25

Состояния системы:

S_0,0 – система свободна (нет очередей и нет обслуживания);

S_0,1 – одна заявка с низким приоритетом;

S_0,2 – две заявки с низким приоритетом;

S_0,n – n заявок с низким приоритетом;

S_1,0 – одна заявка с высоким приоритетом;

S_2,0 – две заявки с высоким приоритетом;

S_m,0 – m заявок с высоким приоритетом;

S_i,j – i заявок с высоким и j заявок с низким приоритетом.

Система уравнений здесь будет такой

        

                      (m > 0);

        (n > 0);

   (m > 0, n > 0).

Нормировочное условие

§  .

§   ;      .

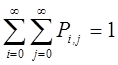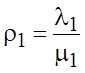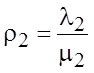§   Условия существования стационарного режима: .

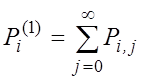§  – вероятность того, что в системе ровно i заявок с первым приоритетом (PR1).

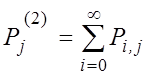§    – вероятность того, что в системе ровно j заявок со вторым приоритетом (PR2).

§   Заявки с первым приоритетом как бы не замечают заявок второго приоритета. Как только приходит заявка первого приоритета – она сразу обслуживается. Поэтому

.

§   Среднее число заявок в системе, обладающих PR1

.

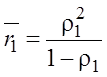§   Среднее время пребывания заявки  с PR1  в очереди

.

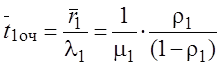§   Среднее время пребывания заявки с PR1 в системе

.

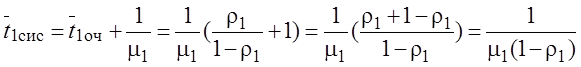§  Среднее число заявок с приоритетом PR2 в очереди

.  

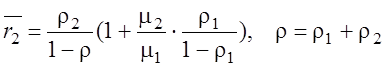§   Среднее время нахождения в очереди заявки с PR2

.

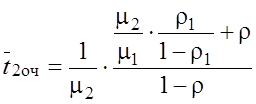§   Среднее время нахождения в системе заявки с PR2

.

2.5.2. Назначение приоритетов

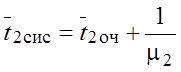Пусть система обслуживает i типов заявок (i= ), каждый тип образует входной поток с параметром . Длительность обслуживания заявок i–го типа – случайная величина с плотностью распределения , имеющая математическое ожидание b_i и дисперсию .

Оптимальные приоритеты устанавливаются по критерию минимума потерь

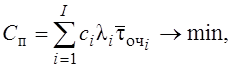
где c_i – потери при ожидании обслуживания в относительных единицах.

Условие оптимальности относительных приоритетов

                                                      (1)

При абсолютных приоритетах с дообслуживанием прерванной заявки оптимальными являются приоритеты, удовлетворяющие дополнительно условиям

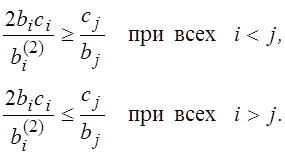
При выполнении этих неравенств оптимальные абсолютные приоритеты лучше, чем оптимальные относительные приоритеты.

Если все эти неравенства не выполнены, то оптимальные относительные приоритеты лучше оптимальных абсолютных приоритетов. Если же часть этих неравенств выполнена, то соответствующие потоки должны иметь абсолютный приоритет, а остальные – относительный.

Если потоки перенумерованы в соответствии с неравенствами (1), то значения , минимизирующие С_п, имеют простой вид

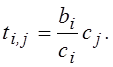
Это эквивалентно таким правилам выбора заявок на обслуживание:

– в первую очередь обслуживать ту заявку, у которой отношение  минимально. Здесь  есть время дообслуживания заявки.

– При равенстве c_i  в первую очередь обслуживать ту заявку, у которой b_i минимально.

Сравнивать введенные приоритеты можно по среднему времени ожидания заявок типа j.

Пусть приоритеты установлены в соответствии с номерами потоков: самый высокий у первого, затем у второго и т. д.

При относительных приоритетах среднее время ожидания заявок типа j равно

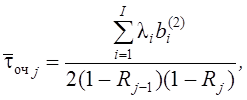
где  – коэффициент загрузки системы всеми заявками от 1–го до j–го типа включительно:

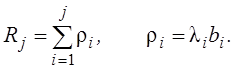
При абсолютных приоритетах с дообслуживанием прерванной заявки среднее время ожидания начала обслуживания 

2. 6. Многофазные системы

2.6.1. Двухфазная система с отказами

Рассмотрим одноканальную двухфазную систему массового обслуживания с отказами при разной производительности приборов (рис. 26).

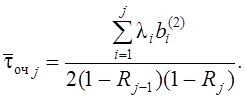
Рисунок 26

Обозначим состояния системы:

S₀₀ – первый и второй приборы свободны от обслуживания;

S₁₀ – первый прибор занят обслуживанием, второй свободен;

S₀₁ – первый прибор свободен, второй занят обслуживанием;

S₁₁ – оба прибора заняты обслуживанием.

Граф переходов системы показан на рис. 27.

В стационарном режиме система описывается следующими уравнениями