Структура систем массового обслуживания. Входной поток заявок. Приборы (каналы) обслуживания. Показатели эффективности СМО, страница 14

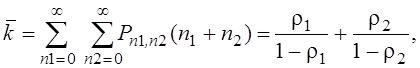
при этом среднее число заявок, находящихся в первой фазе, равно

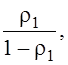
а во второй фазе

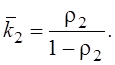
Сравним параметры двухфазной системы с параметрами однофазной системы.

§  Вероятность того, что приборы свободны от заявок

§  Вероятность того, что в первой фазе находится n₁ заявок, а во второй ни одной

§  Математическое ожидание числа заявок, находящихся в системе

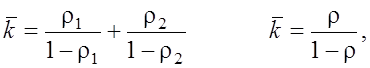
при этом среднее число заявок, находящихся в первой и второй фазе, равно соответственно

   

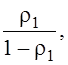
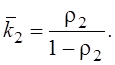
Как видим, при стационарном режиме получается, что обе фазы ведут себя так, как будто бы у них на входах один и тот же поток заявок с параметром .

3. Многоканальные системы массового обслуживания

3.1. Схема «гибели и размножения»

Во многих системах массового обслуживания граф переходов может быть представлен так, как показано на рис. 30. Пусть в графе переходов всего n+1 состояний.

И пусть существуют конечные вероятности состояний P₀, P₁,… P_n, где P_i – не зависит от времени (стационарный режим).

Рис. 30

Система уравнений составляется стандартно:

для  S₀:  

для  S₁:   

…

для  S_n:

Из первого уравнения получаем:

;

…

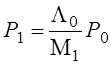Для упрощения рассмотрим систему, где n = 2.

Граф переходов этой системы показан на рис. 31.

Система уравнений

                                                                             (1)

                                                        (2)

                                                                                (3)

P₀ + P₁ + P₂ = 1.                                                                                  (4)

Рисунок 31

Решаем систему:

Из  (1) 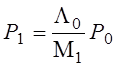        = α₁ P₀,            где α₁ = .

Из (3) 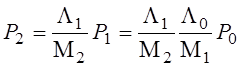 = α₂ P₀,  где α₂ = .

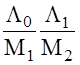Примем, что        P₀  = α₀ P₀,              где α₀ = 1.

Из уравнения (4) находим      α₀P₀ + α₁P₀ + α₂P₀ = 1.

Откуда получаем          _.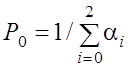

В общем случае

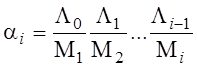 ;    α₀=1.

.

.   

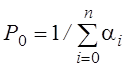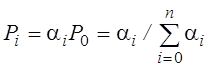Выражения в рамке – это общий вид решения для многих СМО.

3.2. Система с отказами

Рассмотрим систему М/М/n/0, схема которой показана на рис. 32.

Граф переходов системы приведен на рис. 33.

Здесь мы имеет точную копию схемы “гибели и размножения” (см. рис. 26) с параметрами

,            .

Используем полученные ранее результаты

…

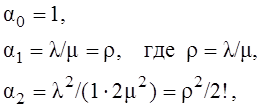
Следовательно,

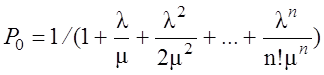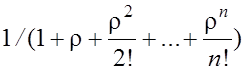 =  = 1/.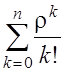

 Рисунок 32

 Рисунок 33

Для вероятностей других состояний получаем

 ;            

;         

;  

…

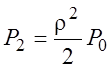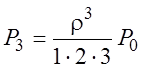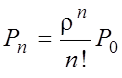 – все n приборов заняты.

Параметры системы

§  Вероятность отказа в приеме заявки на обслуживание

P_отк = P_n;

§  Относительная пропускная способность, т.е. доля обслуженных заявок

q = 1 – P_отк = 1 – P_n.

§  Абсолютная пропускная способность   

А = λq – среднее число обслуженных заявок в единицу времени.

§  Среднее число занятых устройств

.

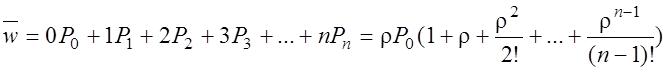Среднее число занятых устройств можно определить иначе – абсолютная пропускная способность A – это интенсивность обслуживания заявок системой в целом,  – интенсивность обслуживания заявок одним прибором, поэтому

.

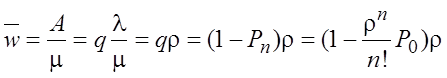Пример.

Определить характеристики системы M/M/3/0 (рис. 34).

Граф переходов системы показан на рис. 35.

t_обс = 2 минуты на заявку, следовательно   заявки/мин, интенсивность поступления заявок  = 1,5 заявки/мин.

Все потоки простейшие. Система с потерями.

Найти: P_отк, q, A,.

Для одного обслуживающего прибора     .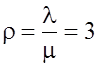

Для трех приборов 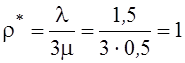                  – предельный случай.

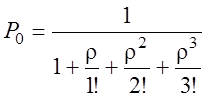,      P₀;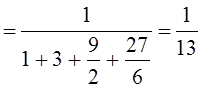  

Рисунок 34

Рисунок 35

;              ;                    .

;            ;            .

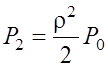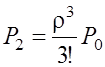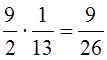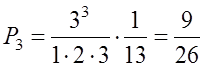Вероятность отказа  P_отк  = P₃ = .

Относительная пропускная способность

q = 1 – P_отк = 1 – .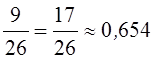

Абсолютная пропускная способность

А = q  заявки/мин.

Среднее число занятых устройств

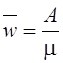 = q= 0,981/0,5 = .

3.3. Два последовательно расположенных прибора разной производительности

Пусть имеем два прибора, например, контрольные стенды разной производительности расположенные друг за другом у транспортера поточного производства и выполняющие одну и ту же операцию (рис. 36).