Структура систем массового обслуживания. Входной поток заявок. Приборы (каналы) обслуживания. Показатели эффективности СМО, страница 13

Рисунок 27

Решение этой системы уравнений проведем следующим образом.

Прежде всего, упростим систему. Для этого из первого уравнения найдем P₀₀  и подставим полученное выражение во второе и последнее уравнения. Получаем

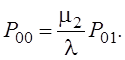                                                                                                 (1)

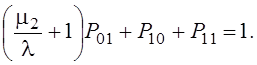
Замечаем, неизвестных 3, а уравнений 4, следовательно, одно уравнение можно исключить, последнее уравнение исключать нельзя, поэтому исключим второе уравнение, как наиболее сложное. Запишем систему уравнений в упорядоченном виде

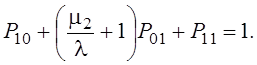
Решение будем искать по правилу Крамера (через определители)

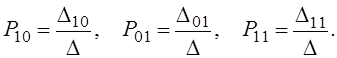
Здесь  определитель системы

 = –,

    определитель для P₁₀

 = ,

   определитель для P₀₁

 = ,

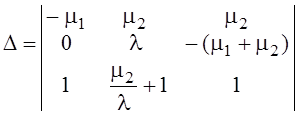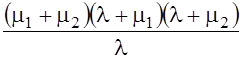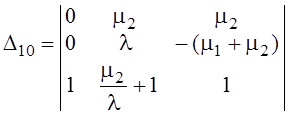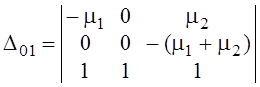    определитель для P₁₁

 = .

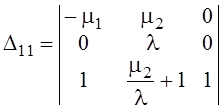Таким образом, получаем

§  Вероятность того, что занят обслуживанием только первый прибор

.

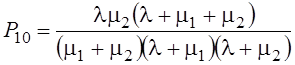§  Вероятность того, что занят обслуживанием только второй прибор

.

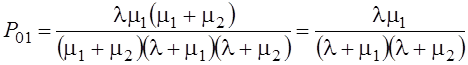§  Вероятность того, что заняты оба прибора

.

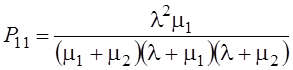§  Вероятность того, что все приборы свободны от обслуживания, найдем из уравнения (1)

= .

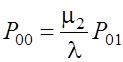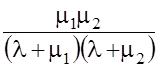Определим относительную и абсолютную пропускные способности системы.

Первый прибор отказывает заявке в обслуживании, если он занят обслуживанием другой заявки, а занят он в состояниях S₁₀ и S₁₁, поэтому

q₁ = 1 – (P₁₀ + P₁₁).

§  Абсолютная пропускная способность первого прибора равна

A₁ = .

§  Абсолютная пропускная способность первого прибора есть интенсивность потока заявок, поступающих на второй прибор.

Второй прибор занят в состояниях S₀₁ и S₁₁, поэтому

q₂ = 1 – (P₀₁ + P₁₁).

§  Абсолютная пропускная способность второго прибора и системы в целом равна

A₂ = A₁q₂ = q₁q₂ = (1 –P₀₁ – P₁₁)(1 – P₀₁ – P₁₁).

Анализ этого выражения позволяет сделать вывод о том, что производительность системы не зависит от распределения приборов разной производительности по фазам. (Производительность системы определяется произведением q₁q₂.) Это означает, что пропускная способность системы определяется ее ”слабым звеном”. Если производительность одной из фаз очень мала по сравнению с другими, то эта фаза и будет определять пропускную способность системы.

2.6.2.Двухфазная система без потерь

Рассмотрим одноканальную двухфазную систему массового обслуживания без потерь, состоящую из двух приборов разной производительности (рис. 28). Время обслуживания приборами заявок подчинено показательному закону распределения с параметрами  и  соответственно для первого и второго приборов. Поступившее в систему требование вначале обслуживается первым прибором. Если он уже занят, то требование ожидает своей очереди до тех пор, пока все ранее пришедшие требования не будут обслужены. После обслуживания первым прибором требования поступают на второй. Так же как и в первом приборе, они поступают на обслуживание, если второй прибор свободен. Если прибор занят, то требование становится в очередь. Входной поток заявок пуассоновский с интенсивностью .

Граф переходов у этой системы бесконечен. На рис. 29 показаны наиболее важные фрагменты графа, по которым можно написать уравнения состояний системы

. . .

. . .

. . .

. . . где     Р₀₀ –  вероятность того, что оба прибора свободны;

Р_n1,n2—вероятность состояния системы, при котором в первой фазе находится n₁ заявок, а во второй фазе – n₂ заявок (включая и те, которые уже обслуживаются).

Рисунок 28

Решение системы этих уравнений достаточно сложно, поэтому приведем конечные результаты:

§  Вероятность того, что оба прибора (обе фазы) свободны от заявок

Рисунок 29

§  Вероятность того, что в первой фазе находится n1 заявок, а во второй ни одной

.

§  Вероятность того, что во второй фазе имеется n₂ заявок, а в первой ни одной

.

§  Вероятность того, что в первой фазе находится n₁ заявок, а во второй фазе n₂ заявок

.

§  Математическое ожидание числа заявок, находящихся в системе