Структурная схема этой системы аналогична схеме системы М/М/1/1, только длина очереди не 1, а m. Граф переходов системы показан на рис. 21.
Система имеет m + 2 состояния:
S0 –система свободна;
S1–прибор занят, очереди нет;
S2– в очереди 1 заявка;
S3– в очереди 2 заявки;
…
Sm – в очереди m – 1 заявка;
Sm+1– в очереди m заявок (очередной заявке отказ).
Система уравнений:
–λ P0 + µ P1 = 0;
λ P0 –( λ+µ) P1 +µ P2 = 0;
λ P1 – ( λ +µ) P2 + µ P3 = 0;
…
λ Pm–1 – ( λ +µ) Pm + µ Pm+1 = 0;
λ Pm – µ Pm+1 = 0;
P0 + P1 + P2 + … + Pm + Pm+1 = 1.
Используя результаты, полученные для системы М/М/1/1, здесь будем иметь
P1 = ρ P0;
P2 = ρ2 P0;
P3 = ρ3 P0 ;
…
Pm = ρm P0;
Pm+1 = ρm+1 P0.
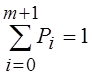 .
.
P0![]() =1/(1+ ρ+ ρ2+ ρ3 +.... + ρm+1) = (1 – ρ)/(1 – ρm+2), так как в знаменателе
снова имеем геометрическую прогрессию с первым членом, равным 1, и знаменателем
ρ<>1.
=1/(1+ ρ+ ρ2+ ρ3 +.... + ρm+1) = (1 – ρ)/(1 – ρm+2), так как в знаменателе
снова имеем геометрическую прогрессию с первым членом, равным 1, и знаменателем
ρ<>1.
§ Вероятность простоя системы
P0![]() = (1 – ρ)/(1 – ρm+2),
= (1 – ρ)/(1 – ρm+2),
§ Вероятность потерь
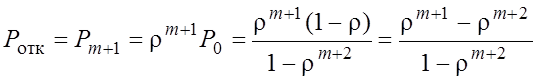 ,
ρ<>1.
,
ρ<>1.
§ Относительная пропускная способность (доля обслуженных заявок)
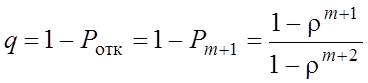 .
.
§ Абсолютная пропускная способность
А = λq – интенсивность потока обслуженных заявок.
§
Среднее число заявок в очереди ![]() .
.
Вероятности соответствующего числа заявок в очереди:
– нет заявок в очереди P0 + P1,
– одна заявка в очереди P2,
– две заявки в очереди P![]() 3 и т.д.
3 и т.д.
![]() = 1ρ2P0
= 1ρ2P0![]() + 2 ρ3P0 +...+ m ρm+1P0 = ρ2 P0(1 + 2ρ +...+ mρm–1) =
+ 2 ρ3P0 +...+ m ρm+1P0 = ρ2 P0(1 + 2ρ +...+ mρm–1) =
= ρ P0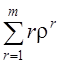 =
=
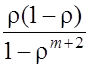
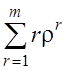 .
.
Ряд, представленный в полученном выражении суммой, можно свернуть, но получаемая при этом формула сложна. Вот что получается
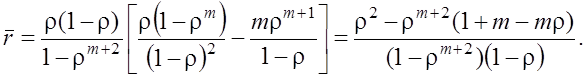
При вычислениях (особенно на компьютере) удобнее воспользоваться выражением
![]() =
ρ P0
=
ρ P0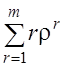 .
.
§ Среднее число заявок на обслуживании:
Нет заявок на обслуживании в состоянии S0, а в остальных состояниях на обслуживании находится одна заявка (и когда нет очереди, и когда она есть!).
![]() = 0 P0 + 1(1 – P0).
= 0 P0 + 1(1 – P0).
Для вероятности 1– P0 получаем
1 – P0![]() = ((1 – ρm+2) – (1 – ρ))/(1 – ρm+2) = (ρ –
ρm+2)/(1 – ρm+2).
= ((1 – ρm+2) – (1 – ρ))/(1 – ρm+2) = (ρ –
ρm+2)/(1 – ρm+2).
Поэтому
![]() = (ρ – ρm+2)/(1 – ρm+2).
= (ρ – ρm+2)/(1 – ρm+2).
§ Среднее число заявок в системе (в очереди и на обслуживании):
![]() .
.
§ Среднее время ожидания в очереди определяется из следующих соображений.
первая заявка в очереди ждет, пока будет обработана заявка, находящаяся на обслуживании в приборе, вторая заявка в очереди ждет, пока будут обработаны заявка, находящаяся в приборе, и первая заявка в очереди, т.е. пока будут обработаны две заявки, и т.д.
Вероятность нахождения заявки в приборе равна P1, вероятность нахождения заявки на первом месте в очереди равна P2 и т.д.
Воспользовавшись формулой оценки математического ожидания случайной величины, получаем
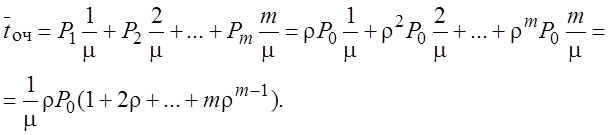
Умножив и разделив это выражение на ρ, получаем
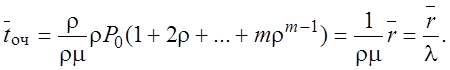
§ Среднее время пребывания заявки в системе
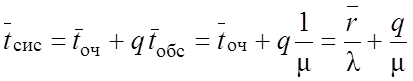 .
.
Это система М/М/1/∞, в которой очередь не ограничена.
Граф переходов и система уравнений здесь бесконечны, поэтому параметры системы получим следующим образом.
Для системы с очередью длины m имеем
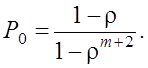
Если устремить m к
бесконечности, то ![]() , так как
, так как ![]() .
Поэтому
.
Поэтому
![]() = 1 – ρ;
= 1 – ρ;
P1 = ρ ![]() = ρ(1 – ρ);
= ρ(1 – ρ);
P2 =
ρ2![]() = ρ2(1 – ρ);
= ρ2(1 – ρ);
…
Pk = ρk ![]() = ρk(1 – ρ).
= ρk(1 – ρ).
…
§
![]() – средняя длина очереди.
– средняя длина очереди.
Выражение получено следующим образом:
в S0 и S1 очереди нет, поэтому
![]() = 1P2+2P3+…+kPk+ …= 1ρ2(1– ρ) + 2ρ3(1– ρ) +...+kρk(1– ρ)+…=
= 1P2+2P3+…+kPk+ …= 1ρ2(1– ρ) + 2ρ3(1– ρ) +...+kρk(1– ρ)+…=
= ρ(1– ρ)(ρ + 2ρ2 + 3ρ3 +...+ kρk+…) = ρ(1– ρ) ρ/(1– ρ)2 = ρ2/(1– ρ).
ПРИМЕЧАНИЕ: Сумма бесконечно убывающей геометрической прогрессии с первым членом ρ и общим членом kρ k равна ρ/(1 – ρ)2.
§ q = 1 – вероятность того, что заявка будет обслужена, равна 1 (очередь не ограничена, нет потерь);
§ А = λ.
§
![]() =
=
![]() P0+
P0+![]() (1
– P0) = 0 + (1 – 1+
ρ) = ρ – среднее число заявок на обслуживании.
(1
– P0) = 0 + (1 – 1+
ρ) = ρ – среднее число заявок на обслуживании.
§
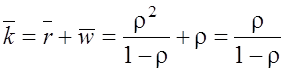 –
среднее число заявок в системе.
–
среднее число заявок в системе.
§
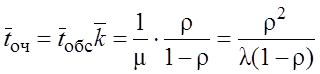 ;
;
![]() обс=1/µ.
обс=1/µ.
§
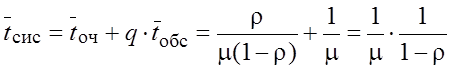 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.