Структура систем массового обслуживания. Входной поток заявок. Приборы (каналы) обслуживания. Показатели эффективности СМО, страница 19

P₂ = α₂ P₀ = 3 ρ² P_{0 ;}            P₂ =  = 0,006479;

P₃ = α₃ P₀ = ρ³ P₀ ;          P₃ =  = 0,000108.

Производительность ВС:

Пр = 1,0P₀ + 0,5P₁ + 0(P₂ + P₃).

Подставляя значения вероятностей, получаем

Пр = 0,863837 + 0,50,129576 + 0 = 0,928625  (92,8625%)

3.7.2. Надежность восстанавливаемых объектов

Предположим, что имеем одно техническое устройство (m = 1) и, как и прежде, поток отказов (заявок) устройства пуассоновский с интенсивностью . обслуживается оно одним каналом, поток обслуживаний пуассоновский с интенсивностью .

Граф переходов для этого случая показан на рис. 49.

Рисунок 49

Этот граф переходов похож на граф одноканальной СМО с потерями, но “заявки” здесь не приходят извне, а порождаются внутри системы. Несмотря на это различие, метод нахождения вероятностей состояний будет таким же, что и для СМО с потерями (см. раздел 2.1.2).

Вероятности состояний характеризуют надежность устройства:

P₀(t) – вероятность застать устройство в момент времени t исправным (работоспособным),

P₁(t) – вероятность застать устройство в момент времени t неисправным (неработоспособным).

В теории надежности эти вероятности носят названия нестационарный коэффициет готовности K_г(t) и нестационарный коэффициет простоя K_п(t) соответственно.

Как и у всякой СМО, здесь можно наблюдать нестационарный и стационарный режимы функционирования. При стационарном режиме вероятности состояний не зависят от времени и носят названия коэффициента готовности K_г и коэффициента простоя K_п.

Другими показателями надежности восстанавливаемых объектов являются – вероятность безотказной работы в течение некоторого времени t – P(t) и вероятность отказа за время t – Q(t), среднее время до первого отказа T₀ и среднее время между отказами T_мо. Эти параметры определяют по графу с поглощающим состоянием, показанному на рис. 50.

Порядок определения P(t), Q(t), T₀, T_мо обычный

–  составление графа,

–  составление системы дифференциальных уравнений,

–  решение системы дифференциальных уравнений.

Составленный граф показан на рис. 50.

Рисунок 50

Система дифференциальных уравнений здесь будет такой

 

Для решения этой системы воспользуемся преобразованиями Лапласа (см. раздел 2.1.1).

Из первого уравнения получаем

В уравнении одно неизвестное, поэтому его можно решить независимо от других уравнений.

При начальных значениях P₀(0) = 1, P₁(0) = 0 находим

Обратное преобразование дает

.

В теории надежности вероятность P₀(t) обозначают просто P(t) и называют вероятностью безотказной работы.

P₁(t) найдем из нормировочного уравнения

.

В теории надежности эту вероятность называют вероятностью отказа и обозначают Q(t).

В нашем случае вероятность безотказной работы устройства и вероятность отказа в течение времени t равны

.

.

Для определения T₀ воспользуемся аналогией между преобразованием Лапласа функции  и математическим ожиданием времени до отказа.

По определению преобразование лапласа функции P(t) равно

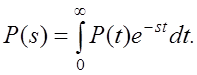
В теории надежности доказано, что математическое ожидание времени до отказа равно

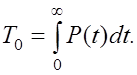
Сравнивая выражения для P(s) и Т₀, замечаем, что Т₀ можно получить из выражения P(s), если в последнем положить s = 0.

Для P(s) имеем

P(s)= 

Заменив здесь s нулем, для Т₀ получаем

Т₀ = 1/.

Для нахождения среднего времени между отказами Т_мо необходимо решить систему дифференциальных уравнений (точнее получить выражение для P(s)) при начальных условиях

Р₀(0) = K_г, P₁(0) = K_п, где K_г – коэффициент готовности, K_п – коэффициент простоя.

Решая, находим

P(s) = P₀(s) = K_г/(s +).

Следовательно, для среднего времени между отказами получаем

Tмо = K_г/.