Структура систем массового обслуживания. Входной поток заявок. Приборы (каналы) обслуживания. Показатели эффективности СМО, страница 11

Система состоит из буферной памяти объемом m и блока обработки. Заявки поступают в буфер с интенсивностью  (поток заявок пуассоновский), где накапливаются. Если буфер полон, то очередная заявка теряется. Вся информация из буфера (полон он или нет) поступает в блок обработки, если в нем закончилась обработка предыдущего массива информации. Длительность обработки массива заявок случайна и распределена по показательному закону с интенсивностью .

Структурная схема системы показана на рис. 22 , а граф ее переходов на рис. 23.

 Рисунок 22

Рисунок 23

Состояния системы свяжем с количеством заявок в буфере.

Система уравнений здесь будет такой

– P₀ +  = 0,

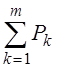P₀ – ( + )P₁ = 0,

   …

P_m–2 – ( + )P_m–1 = 0,

P_m–1 – P_m = 0.

Так как 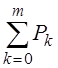       = 1, то 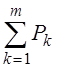 = 1 – P₀.

Подставив это выражение в первое уравнение, получаем

– P₀ + (1–P₀) = 0.

Откуда

P₀ = /( + ) = 1/(/ + 1) = 1/(+ 1),  где      = /.

Для вероятностей других состояний получим

P_k = ^k/( + 1)^k+1  при k < m,

P_m = ^m/( + 1)^m.

Потеря заявки в системе происходит только тогда, когда буфер полон, поэтому вероятность отказа здесь будет равна P_m, т.е.

P_отк = P_m = ^m /( + 1)^m.

Среднее число заявок, находящихся в буфере, определяется из выражения

 = .

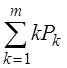Учитывая, что среднее значение времени обслуживания определяется временем обслуживания среднего числа заявок, принимаемых из буфера на обслуживание, можно определить среднее время, которое тратит прибор на обслуживание одной заявки,

= 1/().

Используя формулу для определения вероятности P_m, можно найти необходимый объем буферной памяти при заданной надежности обслуживания                 (1 – P_отк),  производительности прибора  и интенсивности входного потока

m = ln P_отк/[ln – ln ( + 1)] .

Пример.

Требуется определить объем буферной памяти в системе, аналогичной рассмотренной, если  = 10 заявок/сек,  = 0,1 заявки/сек, а вероятность потери заявки не должна превышать P_отк = 0,01 (1% от поступающих сообщений).

Определяем         = / = 10/0,1 = 100.

Определяем объем буфера     m = ln 0,01/[ln100 – ln(100 + 1)]  463.

2.5. Системы с приоритетами

При создании автоматизированных информационных и управляющих систем стремятся так организовать систему сбора и обработки информации, чтобы извлечь максимум информации из потоков сообщений разной интенсивности и значимости. В этих системах задержки в обслуживании приводят к потерям, которые зависят от степени важности заявок. Минимизация потерь достигается назначением оптимальных приоритетов для разных заявок. При этом требуется также произвести выбор между относительными, абсолютными и смешанными приоритетами.

При относительных приоритетах появление в очереди заявки более высокого приоритета, чем выполняемая не прерывает выполнения последней. В момент окончания обслуживания из ожидающих заявок выбирается заявка с самым высоким приоритетом, а если их несколько – то та, которая поступила раньше.

При абсолютных приоритетах появление заявки более высокого приоритета прерывает обслуживание заявки с меньшим приоритетом и обслуживается поступившая заявка. В момент освобождения канала обслуживания из ожидающих заявок выбирается заявка с самым высоким приоритетом, а если их несколько, то та, которая поступила раньше. Таким образом, абсолютные приоритеты действуют в двух случаях: при поступлении заявок и при освобождении канала, а относительные – только во втором случае.

Возможно введение смешанных приоритетов, занимающих промежуточное положение между абсолютными и относительными приоритетами.

2.5.1. Система с абсолютным приоритетом

Рассмотрим систему (рис. 24), на вход которой поступают два потока заявок, интенсивности поступления и обслуживания заявок разные λ₁, λ₂, µ₁ и µ_2.

Входные потоки – пуассоновские.

Обе очереди неограниченны: m₁  и  m₂.

Приоритет потока 1 – абсолютный, т.е. как только появляется заявка 1–ого потока, обслуживание заявки 2–ого потока прекращается.