Структура систем массового обслуживания. Входной поток заявок. Приборы (каналы) обслуживания. Показатели эффективности СМО, страница 20

Рассмотрим теперь резервированное восстанавливаемое устройство, которое состоит из k элементов, выполняющих основную работу, и l резервных, так что общее число элементов в устройстве равно m. Интенсивности отказов элементов одинаковые и равны . Отказавшие элементы направляются в ремонт. Возможен также режим, когда в ремонт отправляется только устройство целиком, если в нем не осталось исправных элементов, а в рабочее состояние устройство переводится только после восстановления всех его элементов. Ремонтом элементов могут заниматься n бригад, причем каждая бригада ремонтирует один элемент. Интенсивности восстановления у всех бригад одинаковые и равны .

В теории надежности различают нагруженный (горячий) резерв и ненагруженный (холодный) резерв. При горячем резерве резервные элементы находятся в рабочем режиме и могут отказывать так, как и основные. При холодном резерве резервные элементы выключены и не отказывают. (В действительности отказы элементов могут происходить в любом состоянии, но в выключенном состоянии интенсивность отказов много меньше интенсивности отказов в рабочем состоянии, поэтому условно ее можно принять равной нулю.)

Если число ремонтных бригад n = 1, то имеем полностью ограниченное восстановление, если число ремонтных бригад , то имеем неограниченное восстановление.

Рассмотрим дублированное устройство, т.е. устройство, в котором имеется один основной (k = 1) и один резервный элемент (l = 1, m = 2).

Состояния системы свяжем с количеством неисправных элементов

S₀ – неисправных элементов в устройстве нет,

S₁ – в устройстве один элемент исправен и один неисправен,

S₂ – оба элемента неисправны.

Рассматривая эксплуатацию устройства как систему массового обслуживания, с учетом возможных видов резервирования и восстановления получаем варианты графов переходов системы, показанные на рис. 51.

Эти графы, за исключением графов с полным восстановлением, можно представить в виде схемы "гибели и размножения" рис. 52,а.

Как было показано в разделе  2.1.1, переходной процесс в СМО продолжается 2  3 , где  , а у надежных устройств , поэтому определять нестационарные коэффициенты готовности и простоя не будем.

Рассматриваемое устройство сохраняет работоспособность в состояниях S₀ и S₁, поэтому стационарный коэффициент готовности (вероятность застать устройство работоспособным) будет равен сумме вероятностей P₀ и P₁

K_г = P₀ + P₁.

Устройство перестает быть работоспособным в состоянии S₂, поэтому коэффициент простоя равен

K_п = Р₂.

Так как граф рис. 52,а аналогичен графу  рис. 31, то

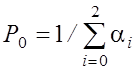, где α₀  = 1,   α₁ = ,     α₂  = .

, 

.

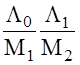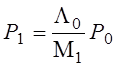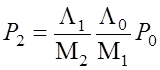Рисунок 51,а. Горячий резерв, полностью ограниченное восстановление

Рисунок 51,б. Горячий резерв, неограниченное восстановление

Рисунок 51,в. Горячий резерв, полное восстановление

Рисунок 51,г. Холодный резерв, полностью ограниченное восстановление

Рисунок 51,д. Холодный резерв, неограниченное восстановление

Рисунок 51,е. Холодный резерв, полное восстановление

Рисунок 52

Покажем, как можно определить P(t) и Т₀ по графу рис. 52,б при начальных условиях

P₀(0) = 1;   P₁(0) = 0;   P₂(0) = 0.

Напомним, устройство работоспособно в состояниях S₀ и S₁, поэтому вероятность безотказной работы будет равна

P(t) = P₀(t) + P₁(t), а вероятность отказа

Q(t) = P₂(t).

Система дифференциальных уравнений здесь будет такой

,

,

Воспользовавшись преобразованиями Лапласа, получаем

,

,

.

Как видим, вероятности P₀(s) и P₁(s) можно найти из первых двух уравнений. Представим эти уравнения в упорядоченном виде

,

.

Применим правило Крамера

.

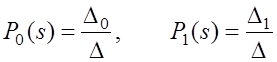где 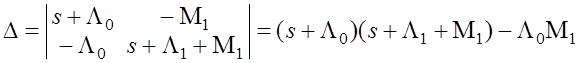  – определитель системы,

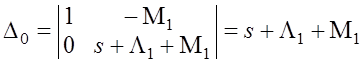 – определитель для вычисления P₀(s),

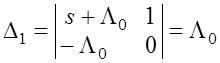 – определитель для вычисления P₁(s).

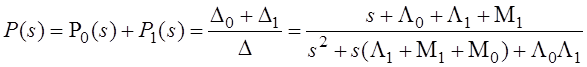.                   (1)

Для получения P(t) необходимо применить обратное преобразование Лапласа. Алгоритм действий здесь таков (пример см. в разделе 2.1.1):