Структура систем массового обслуживания. Входной поток заявок. Приборы (каналы) обслуживания. Показатели эффективности СМО, страница 5

Под качеством работы систем массового обслуживания понимается не то, как хорошо выполнено само обслуживание (качество ремонта, решения задачи и т. д.) – это оценивается другими критериями, – а как хорошо организовано обслуживание, насколько полно загружены обслуживающие приборы, не создается ли большая очередь или не велик ли уход из системы не обслуженных заявок.

1.9. Классификация систем массового обслуживания

Классификацию систем массового обслуживания (СМО) можно проводить по достаточно большому количеству признаков. Ниже приведена классификация по наиболее значимым признакам. СМО представлены в виде структурных схем, где обозначения элементов систем, как правило, не требуют пояснений.

1.  По количеству параллельно работающих устройств:

– Одноканальные  (рис. 1) 

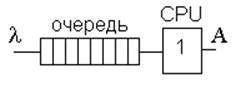Рисунок 1

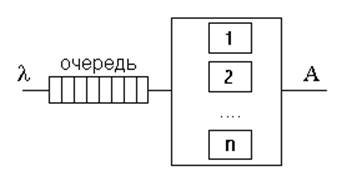
– Многоканальные (рис. 2)

Рисунок 2

На рисунках  и А – интенсивности входного и выходного потоков.

2. 

По количеству последовательно работающих устройств:

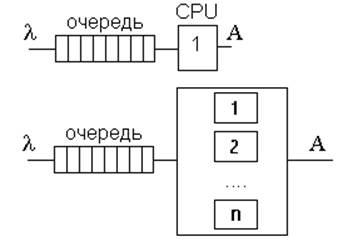–  Однофазные (рис. 3)

Рисунок 3

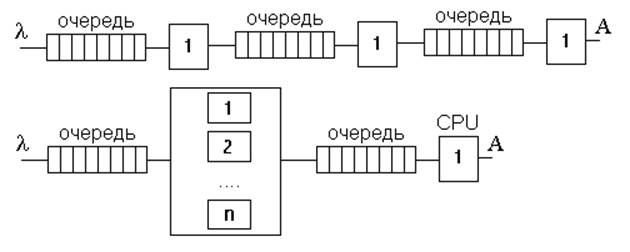
–  Многофазные (рис. 4)

Рисунок 4

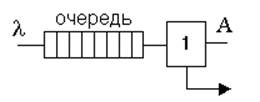
3.  По длине очереди (рис. 5):

а) Длина очереди m = ∞ (без отказов, без потерь);

б) Длина очереди m = 0 (с отказами, потерями);

в) 0 < m < L_max – ограниченная очередь.

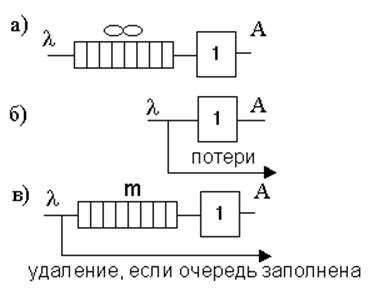
Рисунок 5

4.  По дисциплине обслуживания:

–  FIFO  –  очередь без приоритета.

–  Очередь с относительным приоритетом (рис. 6) – приоритет учитывается только при выборе заявки из очереди.

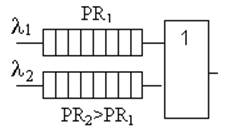
Рисунок 6

При появлении очередной заявки, с более высоким приоритетом, обработка заявки с низким приоритетом не прекращается. Она продолжается до завершения. Обычно приоритеты 1, 2, …М.    1 – наивысший приоритет.

–  Очередь с абсолютным приоритетом (рис. 7) – обслуживание заявки с низшим приоритетом прерывается и обслуживается заявка с абсолютным приоритетом.

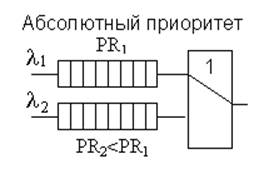
Рисунок 7

–  Возможно введение смешанных приоритетов, занимающих промежуточное положение между абсолютными и относительными приоритетами.

–  LIFO – обслуживается пришедший последним (стек).

5.  По ограничению времени:

–  Ограничение времени ожидания в очереди (рис. 8) – заявка, которая ждет в очереди дольше допустимого времени ожидания, удаляется.

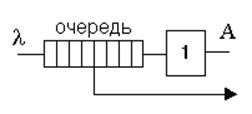
 Рисунок 8

–  Ограничение времени пребывания в системе – удаляется заявка очень долго находящаяся в системе (рис. 9).

 Рисунок 9

6.  По наличию обратной связи

–  Разомкнутые (рис. 3 и другие).

–  Замкнутые

–  Система технического обслуживания (рис. 10).

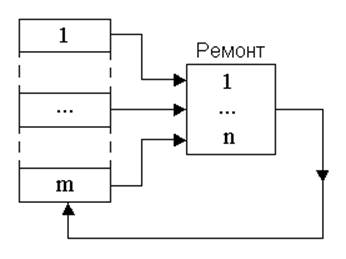
 Рисунок 10

–  Обработка частями – квантами (рис. 11).

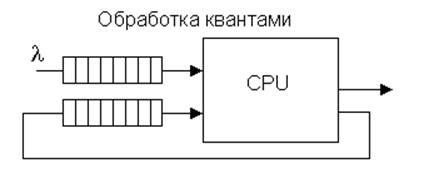
 Рисунок 11

7.  По законам поступления заявок на вход системы

–  Пуассоновское распределение (пуассоновский поток заявок).

Вероятность появления k заявок за время t равна здесь

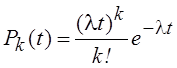, где  – интенсивность поступления заявок.

Для этого закона математическое ожидание M = , дисперсия D = , т.е. M = D – это признак данного закона.

Вероятность того, что заявок за время t не будет

.

Интервалы времени между заявками, поступающими по этому закону, имеют экспоненциальное распределение

, для которого M = ,  D = .

Считается, что пуассоновский поток заявок наихудший.

–  Распределение Эрланга – получается выборкой из пуассоновского потока (берем k–е событие).

Плотность распределения интервалов времени между событиями для этого закона равна

 

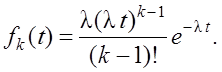
Математическое ожидание и дисперсия здесь равны

M = ,  D = .

Интенсивность поступления заявок этого закона равна

,

где  – интенсивность порождающего потока.

При k = 1 получим экспоненциальное распределение (см. выше).

– Произвольный закон.

– Регулярные события (через заданные, не обязательно одинаковые, интервалы).

Пуассоновский поток заявок

Пуассоновский поток случайных событий (заявок), он же простейший, обладает следующими свойствами:

– стационарностью;