Структура систем массового обслуживания. Входной поток заявок. Приборы (каналы) обслуживания. Показатели эффективности СМО, страница 16

А = λ (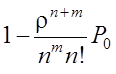) – среднее число обслуженных заявок в единицу времени.

§  Среднее число занятых устройств  определим следующим образом.

Каждый занятый канал обслуживает в среднем  заявок в единицу времени, а вся система в среднем обслуживает А заявок в единицу времени, поэтому, деля последнее на первое, получаем

=А/ = λ ()/ = ().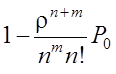

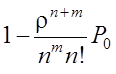§  Средняя длина очереди.

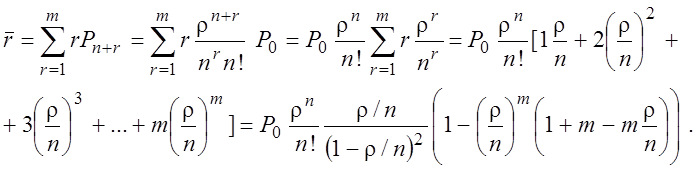
§  Среднее время ожидания в очереди

=  .

§  Среднее число заявок в системе

 _.

§  Среднее время пребывания заявки в системе (время отклика)

.

Это среднее время ожидания в очереди плюс среднее время обслуживания, умноженное на относительную пропускную способность системы.

3.5. Система без потерь

У системы M/М/n/∞ структура такая же, что и у предыдущей, но очередь не ограничена.

Граф переходов системы показан на рис. 40.

Здесь, как и выше, начиная с S_n, все , так как работают все n приборов,  для i = 0, 1, 2,…, .

Функционирование рассматриваемой системы в стационарном режиме, т.е. при  может быть описано системой уравнений

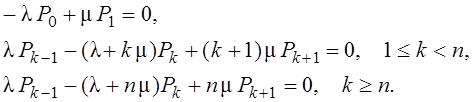
К этим уравнениям необходимо добавить нормирующее уравнение

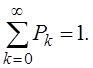
Здесь Р_k – вероятность того, что в системе находится k заявок (k не ограничено).

Рисунок 40

Решая полученную систему алгебраических уравнений, находим следующие параметры системы.

Параметры системы

§  Доля обслуженных заявок

q = 1 – система без потерь.

§  Абсолютная пропускная способность

А = .

§  Вероятность того, что все приборы свободны,

 = .

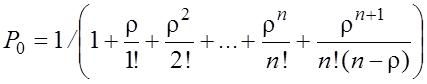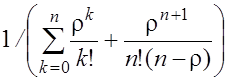При   P₀ = 0.

Выражение 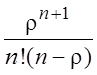 в P₀  получено в результате преобразования бесконечной суммы вероятностей состояний системы, соответствующей бесконечной очереди.

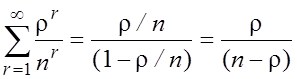 – как сумма бесконечной убывающей геометрической прогрессии с первым членом и знаменателем, равными . Здесь  r – длина очереди.

; 

;

…

;

;

_,

.

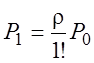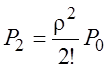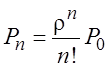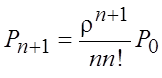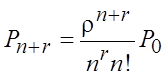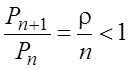§  Средняя длина очереди.

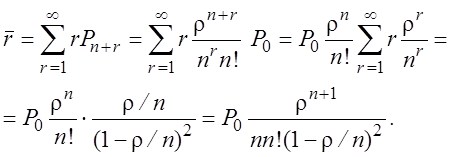
§  Среднее время ожидания в очереди

 = .

§  Вероятность того, что все приборы заняты

 =

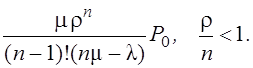
§  Среднее число занятых приборов

. 

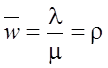Эта формула справедлива для любой СМО с неограниченной очередью.

§  Среднее число заявок в системе

 _.

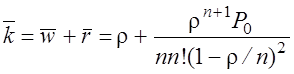§  Среднее время нахождения заявки в системе (время отклика)

  .

Пример. Система M/M/2/ (рис. 41).

Есть две кассы, обслуживающих пассажиров, которые хотят купить билеты на направления А и В.

Интенсивность поступления заявок  заявки/мин.

Среднее время обслуживания пассажира кассой  мин.

Найти: среднюю длину очереди  и среднее время ожидания в очереди .

 Рисунок 41

Интенсивность суммарного входного потока заявок

λ = 0,45 + 0,45 = 0,9 заявок/мин;  интенсивность обслуживания одной кассой

заявок/мин;

интенсивность обслуживания двумя кассами

заявка/мин;

Условие существования стационарного режима:

 = 0,9/0,5 = 1,8 > 1 – одна касса не справляется с суммарным потоком заявок.

При двух кассах .

Состояний у системы неограничено много (рис. 42),

 Рисунок 42

n = 2,

P₁ = ;              P₂ = 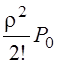;            P₃ = ;

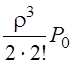P₀=1/(1+ ρ/1! + ρ²/2! + ρ³/(2! (2– ρ))) ;

P₀= 1/(1+ 1,8 + .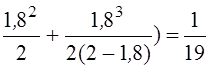

Среднее число занятых устройств

.

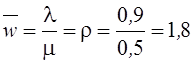Средняя длина очереди

;            .

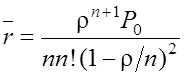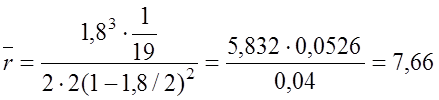Среднее время ожидания в очереди

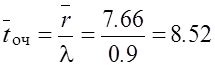 мин.

Поступило предложение:

Разделить поток А + В на два А и В и организовать раздельную продажу билетов (рис. 43).

Условие стационарного режима ;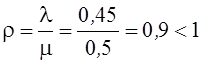

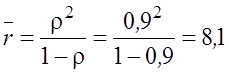 (такие очереди к каждой кассе);

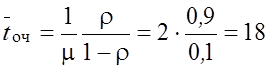 мин.

Рисунок 43

Вывод:

Раздельное обслуживание оказалось хуже:

При совместном обслуживании  = 8,52 мин, при раздельном   = 18 мин .

3.6. Система с очередью и ограниченным временем пребывания заявки в системе

Рассмотрим n–канальную систему рис. 44, в которой заявка, заставшая все n каналов занятыми, может быть обслужена, если за время ее пребывания в очереди освободится хотя бы один канал. Допустимая длина очереди ограничена величиной m. Находясь в очереди, заявка может проявить “нетерпение” и покинуть систему. Поток уходов заявок из очереди имеет интенсивность . Находясь под обслуживанием, заявка может также покинуть систему. Интенсивность потока ухода заявок из под обслуживания равна .