Таким образом регрессионный анализ позволяет на основании небольшого количества экспериментальных данных получить математическую модель ТП, необходимую для его исследования и управления, определения устойчивости его отдельных звеньев, для оценки качества готовой продукции и полуфабрикатов.
2.4 Оптимизация процессов с применением метода крутого восхождения
Эффективным путем оптимизации технологических процессов является применение математического планирования экстремального эксперимента, т.е. метода выбора количества и условий проведения опытов, минимально необходимых для решения задачи оптимазации с требуемой точностью. Нами рассматривается один из самых простых способов планирования, называемый методом крутого восхождения (предложен Боксом и Уилсоном).
В методе используются понятия “факторное пространство” и “поверхность отклика”. Факторным пространством называется пространство с координатными осями, по которым откладываются значения факторов и параметра оптимизации.
Геометрическое изображение функции отклика в факторном пространстве называется поверхностью отклика. Для случая двух факторов возможна наглядная геометрическая иллюстрация поверхности отклика ( при большом числе факторов такая возможность теряется).
Пусть параметр
оптимизации y зависит от
фактора x1
и x2
, т.е факторное пространство задается тремя взаимноперпендикулярными осями.
Наглядное представление о поверхности отклика можно получить по кривым равного
значения параметра оптимизации, называемым линиями равного отклика (рис.2.2).
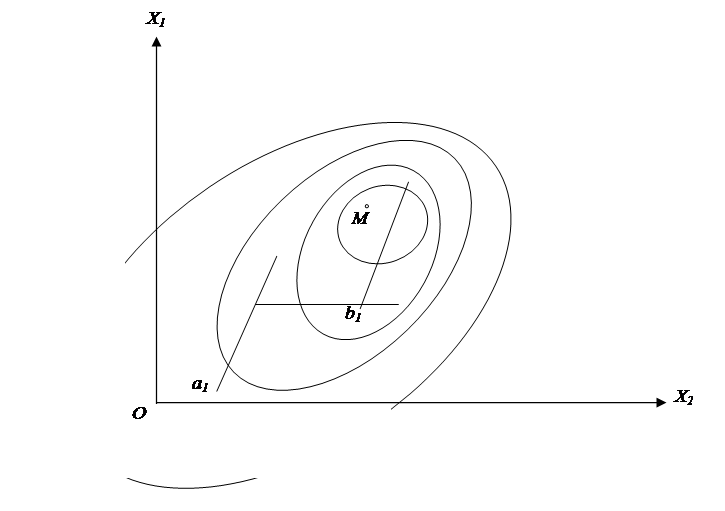
Рис. 2.2
Они являются проекциями на плоскость х1ох2 линий, полученных в сечениях поверхности отклика плоскостями, параллельными плоскостями х1ох2 (т.е. перпендикулярными оси у). Точка М на рисунке – это та оптимальная точка, которую мы ищем.
Сущность метода крутого восхождения заключается в следующем. Около исходной точки а1 (рис.2.2) ставится небольшая серия опытов для определения направления градиента функции отклика. Затем ставятся несколько опытов на линии, совпадающей с этим направлением. Точку b1, в которой значение параметра оптимизации оказалось наилучшим, принимают за новую исходную точку. Указанную процедуру повторяют до тех пор, пока не будет достигнута область оптимума, прилегающая к точке M. После этого в зависимости от конкретной ситуации процесс оптимизации либо заканчивают, либо проводят тщательное изучение области оптимума с целью точного определения координат точки экстремума М.
При планировании эксперимента существенно, какими свойствами обладает объект исследования. Обычно рассматриваются только такие объекты, которые удовлетворяют требованию воспроизводимости результатов эксперимента. Выберем уровни факторов и в этих условиях проведем эксперимент. Затем повторим его несколько раз, через неравные промежутки времени, и сравним полученные значения параметра оптимизации. Если разброс этих значений не превышает некоторой заранее заданной величины (требований к точности эксперимента), то объект удовлетворяет требованию воспроизводимости, а если превышает, то нет.
Перед тем, как приступить к оптимизации технологического процесса, необходимо четко сформулировать цели исследования, выбрать параметр оптимизации и определить факторы, оказывающие существенное влияние на этот параметр.
Движение к оптимуму возможно, если параметр оптимизации только один Однако реальные объекты часто характеризуются несколькими выходными параметрами. Например, изделия могут оцениваться точностью и шероховатостью (детали полученные литьем и точением), сопротивлением и индуктивностью (катушки индуктивности), коэффициентом усиления, входным и выходным сопротивлением (усилитель) и т.д.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.