Планирование экстремальных экспериментов при оптимизации технологических процессов РЕА, страница 19

          При ротатабельном центральном композиционном планировании критерием оптимальности плана является условие одинаковой точности предсказания величины параметра оптимизации в точках, расположенных на равном расстоянии от центра плана. Другими словами, дисперсии параметра оптимизации, вычисленного по найденной модели в указанных точках, должны быть равны.

          Характеристики ротатабельного ЦКП приведены в табл. 2.8. Перевод кодированных координат звездных точек в натуральные значения факторов производится по формуле (2.14).

Таблица 2.8

          В качестве примера в табл.2.9 приведена матрица ротатабельного ЦКП для двух факторов.

Таблица 2.9

          Реализация матрицы ротатабельного ЦКП проводится в соответствии с п.2.4.1.4.

          Коэффициенты полинома определяются по формулам:

          свободный член:

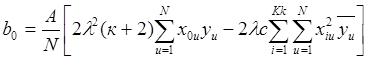                            ;                                          (2.31)

          коэффициенты при квадратичных членах:

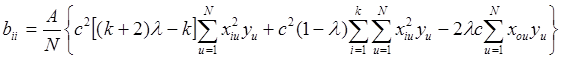                   ;                      (2.32)

          коэффициенты при взаимодействиях:

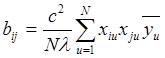                                            ;                                                            (2.33)

          коэффициенты при факторах:

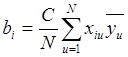                                                 ,                                                                   (2.34)

где

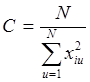                               ,                (i – любое целое число от 1 до к),

,             .

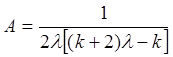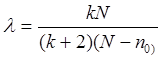          Процедура проверки значимости коэффициентов аналогична описанной в п.2.4.1.5 за исключением пункта, касающегося вычисления оценки дисперсии этих коэффициентов. При  реализации ротатабельных ЦКП дисперсии рассчитываются по формулам:

          Для коэффициентов при факторах и взаимодействиях: