Планирование экстремальных экспериментов при оптимизации технологических процессов РЕА, страница 8

В табл. 2.2   у - у ; у - у ; у - у  данные параллельных испытаний при условии, что факторы (входной параметр) соответственно х11, х12  и х1N   остаются для каждой серии опытов неизменными.

Проверка гипотезы нормальности зависимой переменной в каждом опыте проводится с помощью критерия Пирсона . В тех  случаях, когда гипотеза нормальности не подтверждается, производят преобразование случайной величины, например, логарифмирование. Для преобразованной величины снова проверяется   гипотеза нормальности.

          Выбор критерия для проверки гипотезы однородности дисперсий зависит от числа параллельных наблюдений (наблюдении параметра изделия при одних и тех же условиях ТП) в опыте. Если число параллельных наблюдений для всех опытов  одинаково (наиболее часто встречающийся случай на практике), то гипотеза однородности дисперсий проверяется с помощью критерия Кохрена

maкс

                                              G= ---------------  ;(2.3)

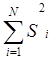
где –значение дисперсии в каждом опыте; макс – ее максимальное значение из опытов. Для этой проверки определяют среднюю арифметическую величину параметра каждого опыта

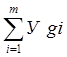
                            =  ----------- .                                                                                  (2.4)

m

(Для данных в табл. 2.2   g =1…). Далее рассчитывают значение дисперсии для каждого опыта:

                                     S= 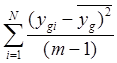.                                              (2.5)

Если рассчитанное значение критерия окажется меньше табличного, то гипотеза об однородности дисперсий принимается. Однородность дисперсий позволяет рассчитать оценку дисперсии воспроизводимости всего эксперимента

S() =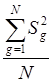.                                                  (2.6)

Расчет коэффициентов регрессии полинома осуществляют, например, методом наименьших квадратов, согласно которому ТП точнее описывает та функция, для которой сумма квадратов отклонений значений переменной   рассчитанных по уравнению регрессии, от экспериментальных значений, минимальна:

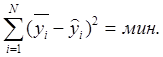
Используя этот прием для полинома по уравнению (2.2), получим:

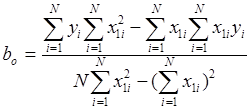;                                     (2.7)

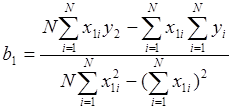.                                          (2.8)

Вычисление коэффициентов регресии проводится на основании ограничеснного числа экспериментальных данных. Поэтому требуется проверить значимость полученных оценок, для чего служит критерий Стьюдента t:

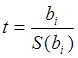,                                                                      (2.9)

где - дисперсия при определении коэффициентов регрессии. Для уравнения (2.2)  рассчитывают:

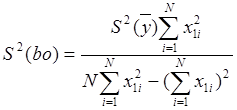
,                                              (2.10)

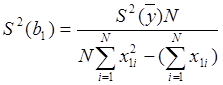.                                                   (2.11)

Если рассчитанная величина критерия превышает табулированное значение , определенное для данного уровня значимости p (0,05; 0,02; 0,01) и числа степеней свободы  f=N(m-1) , то коэффициент  признается значимым. В противном случае коэффициент  считается статистически незначимым. Член полинома с этим коэффициентом можно исключить из уравнения полинома. Далее с учетом этого положения полученное уравнение должно адекватно описывать ТП. Проверка адекватности осуществляется по критерию Фишера:

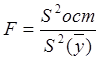 ,                                                            (2.12)

где  Sост –остаточная дисперсия, обусловленная как ошибкой эксперимента, так и взаимным влиянием изучаемых независимых переменных. Она определяется по формуле:

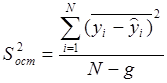,                                                          (2.13) где g - число значимых членов в уравнении регрессии. Уравнение считается адекватным при соблюдении условия , определяемого по таблицам математической статистики для выбранного уровня значимости Р (обычно 0,05) и при заданных числах степеней свободы   и  .

          Если записанное условие не соблюдается, то модель признается неадекватной, и для математического описания ТП необходимо подобрать полином более высокого порядка.