Планирование экстремальных экспериментов при оптимизации технологических процессов РЕА, страница 17

          Если область оптимума далека или ситуация в этом смысле неопределенная, то крутое восхождение продолжают. При этом за новую исходную точку (точку основного уровня для новой серии опытов) принимают ту, в которой были получены наилучшие результаты при осуществлении мысленных опытов.

          Если крутое восхождение оказалось неэффективным, то скорее всего это свидетельствует о том, что модель строилась в области оптимума. Следует поставить несколько опытов в центре плана и определить разность между средним арифметическим значением параметра оптимизации в этих опытах и свободным членом полинома. Если указанная разность окажется значимой, то возможны два решения: закончить исследование, выбрав точку с наилучшим значением параметра оптимизации; перейти к построению и реализации плана второго порядка.

          2.4.1.11 Построение математической модели объекта в почти стационарной области.

          О достижении области оптимума, которую часто называют почти стационарной областью, свидетельствует невадекватность модели в виде линейного или неполного квадратного уравнения, возрастание эффектов взаимодействия, а также значимость разности  между свободным членом полинома и найденным экспериментально значением параметра оптимизации в точке основного уровня.

          Если необходимо найти точные координаты экстремальной точки, то для описания поверхности отклика в почти стационарной области используют полином второго порядка:

,

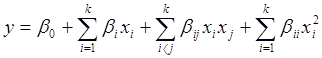где k –число факторов. Например, если k=3, то

.

          Для нахождения раздельных оценок коэффициентов регрессии а приведенном уравнении факторы при постановке экспериментов необходимо варьировать на трех уровнях. Использование планов ПФЭ типа 3оказывается при этом нерациональным из-за слишком большого числа опытов (3). Поэтому для построения модели применяют так называемые центральные композиционные планы (ЦКП), ядром которых являются планы ПФЭ 2. Если математическая модель, построенная с использованием ПФЭ 2, оказалась неадекватной и есть основания считать, что мы находимся в почти стационарной области, то для получения ЦКП второго порядка достаточно добавить к уже имеющемуся плану несколько опытов. Часть из них ставится в центре плана (точке основного уровня), а остальные – в так называемых звездных точках. Количество звездных точек – 2к. Их координаты приведены в табл. 2.5 , где - плечо звездной точки (расстояние от центра плана).

                                                        Таблица 2.5

          Общее количество опытов ЦКП

          N=2+2к+n0,

где 2к - число звездных точек; n0 – число опытов в центре плана.

          Число опытов n0 в центре плана и плечо  выбирается в зависимости от критерия оптимальности, установленного при планировании. По этому признаку различают ортогональные и ротатабельные ЦКП.

          2.4.2 Построение модели объекта с использованием ортогонального ЦКП

          В ортогональном ЦКП критерием оптимальности плана является ортогональность столбцов матрицы планирования.

          В силу этого все коэффициенты регрессии оцениваются независимо друг от друга. Характеристики ортогонального ЦКП приведены в табл.2.6. Перевод кодированных координат звездных точек в натуральные значения факторов производится по формуле (2.14).

Таблица 2.6