Планирование экстремальных экспериментов при оптимизации технологических процессов РЕА, страница 14

          При проведении эксперимента каждая строка матрицы планирования реализуется несколько раз, т.е. ставятся параллельные опыты. После этого вычисляются: среднее арифметическое 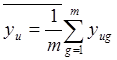                              ,                                                          (2.15)

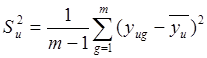                                                      ,                                                (2.16)

где  m – число параллельных опытов (одинаковое для каждой строки матрицы);

U = 1,2,…,N;

N – число строк (опытов) в матрице.

          Построение математической модели исследуемого процесса возможно только в том случае, если дисперсии в строках матрицы окажутся статистически равными, т.е. однородными.

          Гипотеза об однородности дисперсий проверяется по критерию Кохрена. Для  этого:

а) вычисляют величину

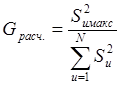                                                      ,                                                  (2.17)

где  - наибольшая из дисперсий;

б) определяют число степеней свободы f1=m-1   и f2=N ;

в) выбирают уровень значимости g (0,05 или 0,10);

г) по числу степеней свободы f1 , f2  при выбранном уровне значимости g определяют величину Gпо таблице приложения 1.

          Если G<G, то гипотеза об однородности дисперсий принимается.

          Для исключения влияния систематических погрешностей, вызываемых внешними неконтролируемыми условиями (изменение характеристик сырья, замена исполнителя и т.д. ), рекомендуется рандомизация опытов, т.е. обеспечение случайной последовательности их выполнения. Для этого, к примеру, все Nm опытов можно пронумеровать, а затем воспользоваться таблицей случайных чисел.

          2.4.1.5 Построение математической модели

          На этом этапе вычисляются коэффициенты полинома, оценивается их статистическая значимость и проверяется адекватность полученной математической модели.

          Коэффициенты полинома при факторах и фиктивной переменной вычисляются по формуле

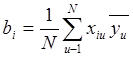                                             ,                                                                (2.18)

где i=0,1,…,к;

к - число факторов.

          Коэффициенты при взаимодействиях вычисляются аналогичным образом.

          Гипотеза о значимости коэффициентов полинома проверяется с помощью t – критерия Стъюдента. Для этого:

а) вычисляют оценку дисперсии параметра оптимизации (дисперсии воспроизводимости эксперимента)

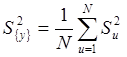                                                         ;                                                           (2.19)

б) вычисляют оценку дисперсии коэффициента полинома

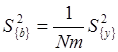                                                         ;                                                              (2.20)

в) всем «n» вычисленным коэффициентам, включая коэффициенты при взаимодействиях и фиктивной переменной, присваивают номера от 1 до n;

г) для каждого из вычисленных коэффициентов определяют  величину

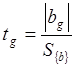                                                      ,                                                               (2.21)

где g=1,2,…n;

д) определяют число степеней свободы f=N(m-1);

е) выбирают уровень значимости g (0,05; 0,10 или 0,20);

ж) по числу степеней свободы f при выбранном уровне значимости g определяют величину  по таблице приложения 2.

          Если < , то g-ый коэффициент незначим. Поэтому взаимодействие (или фактор) с этим коэффициентом следует исключить из уравнения регрессии.

          После отбрасывания незначимых членов проверяется адекватность полученной математической модели. Для этого необходимо вычислить дисперсию адекватности (остаточную дисперсию)

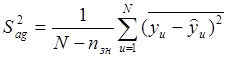                                                      ,                                            (2.22)

где nзн – число значимых членов полинома (оставшихся после отбрасывания незначимых членов);

- значение параметра оптимизации, рассчитанное по математической модели для значений факторов, указанных в u-ой строке матрицы.