Планирование экстремальных экспериментов при оптимизации технологических процессов РЕА, страница 16

          Если область оптимума далека или ситуация неопределенная, то принимается решение о движении по градиенту.

          Во втором случае, если область оптимума близка, то типичное решение – переход к построению плана второго порядка.

          Если область оптимума далека или ситуация неопределенная, то принимается решение о движении по градиенту. Чтобы определить направление градиента, необходимо получить адекватную модель. Для этого следует уменьшить интервалы варьирования факторов и поставить новую серию опытов.

          2.4.1.10 Крутое восхождение по поверхности отклика

          Напомним, что градиент непрерывной однозначной функции отклика есть вектор

,

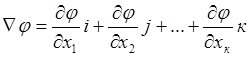где  - обозначение градиента;

 - частная производная функции по i –ому фактору;

i,j,к – единичные векторы в направлении координатных осей.

          Таким образом, для определения направления градиента в какой-либо точке, необходимо найти частные производные функции отклика в этой точке. Изменяя факторы пропорционально значениям частных производных, можно двигаться по градиенту, т.е. в направлении, по которому поверхность отклика изменяется наиболее круто. Поэтому процедура движения к почти стационарной области (области оптимума) называется крутым восхождением.

          Для расчета крутого восхождения необходимо определить частные производные функции отклика в заданной точке (составляющие градиента) и выбрать шаг, через который будут ставится опыты в процессе движения по градиенту.

          В случае линейной модели составляющими градиента в любой точке являются коэффициенты полинома или, если перейти к натуральным значениям факторов хi , произведения bi Ii (здесь Ii – интервал варьирования i- го фактора).

          Для модели в виде неполного квадратного уравнения направление градиента меняется от точки к точке. Градиент целесообразно определять в точке А, где при проведении эксперимента было получено наилучшее значение параметра оптимизации. Для натуральных значений факторов составляющие градиента являются произведениями

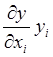 ( здесь - значение частной производной функции отклика по i –ому фактору в точке А). Пусть, например,

и точка А имеет координаты х1 = +1, х2=-1. Тогда

                                                                 

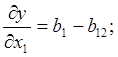
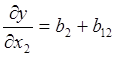
          Фактор, для которого абсолютное значение составляющей градиента оказалось максимальным, принимается за базовый. Для этого фактора выбирается шаг движения по градиенту . Шаги для остальных факторов определяются по формуле

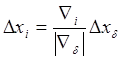                                                            ,                                                      (2.24)

где -составляющая градиента по  i-ому фактору;

- составляющая градиента по базовому фактору.

          Для облегчения работы шаги обычно округляют.

          Качественные факторы в процессе крутого восхождения фиксируют на уровне, при котором было получено лучшее значение параметра оптимизации. Незначимые факторы могут фиксироваться на любом из двух уровней (верхнем или нижнем). При движении по градиенту они не изменяются (в случае линейной модели).

          Последовательным прибавлением найденных шагов к основному уровню (в случае модели в виде неполного квадратного уравнения) получают серию опытов крутого восхождения, которые часто называют мысленными. Далее выделяют мысленные опыты, у которых хотя бы один фактор выходит из интервала

   (здесь -координата основного уровня по i-ому фактору). Некоторые (или все) из этих опытов реализуются.

          Крутое восхождение считается эффективным, если хотя бы в одном из осуществленных мысленных опытов результаты окажутся лучше тех, которые были получены при реализации матрицы планирования. Принимаемые в этом случае решения зависят от того, достигнута или нет область оптимума.

          Если область оптимума достигнута, то возможна окончание исследования или переход к построению и реализации планов второго порядка.