Если ![]() , то модель адекватна.
, то модель адекватна.
Если ![]() , то гипотеза об адекватности модели проверяется
с помощью F- критерия Фишера. Для этого:
, то гипотеза об адекватности модели проверяется
с помощью F- критерия Фишера. Для этого:
а) вычисляют величину
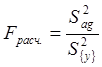 ;
(2.23)
;
(2.23)
б) определяют число степеней свободы f1=N-nзн и f2=N(m-1);
в) выбирают уровень значимости g (0,05 или 0,10);
г) по числу степеней свободы f1 и f2 привыбранном уровне значимости g определяют величину Fтабл. по таблице приложения 3.
Если Fрасч.< Fтабл. , то гипотеза об адекватности модели принимается.
Необходимо подчеркнуть, что проверка адекватности модели указанным способом возможна только в том случае, если N-nзн>0, т.е. имеется избыточность в опытах. В противном случае адекватность можно проверить косвенным путем. Для этого ставится несколько опытов в центре плана (в точке основного уровня) и определяется разность между средним арифметическим значением параметра оптимизации в этих опытах и свободном членом полинома (коэффициентом b0). Если эта разность окажется незначимой, то модель можно считать адекватной.
2.4.1.6 Принятие решений после построения модели
Принимая решения после построения модели, необходимо учитывать многие обстоятельства, важнейшими из которых являются следующие: вид построенной модели (линейное или неполное квадратное уравнение); факт адекватности или неадекватности модели; значимость коэффициентов полинома; информация о положении оптимума (оптимум близко, далеко, или ответить на этот вопрос нельзя). Рассмотрим типичные решения в наиболее часто встречающихся ситуациях.
2.4.1.7 Линейная модель адекватна
Здесь могут быть два варианта: 1 – оптимум далеко или о его положении нет информации, неопределенная ситуация;
2 – оптимум близко.
Типичным решением для первого варианта является движение по градиенту. Движение по градиенту наиболее эффективно, если коэффициенты при всех факторах значимы. Статистическая незначимость коэффициентов может быть обусловлена следующими причинами:
Основной (нулевой)
уровень х![]() близок к точке
частного экстремума по данной переменной (фактору) хi
близок к точке
частного экстремума по данной переменной (фактору) хi
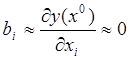 ;
;
интервал варьирования уi был выбран слишком малым;
велика погрешность эксперимента вследствие наличия неуправляемых переменных (факторов);
данный фактор не оказывает влияния на параметр оптимизации (в этом случае его следует зафиксировать и исключить из дальнейшего рассмотрения).
Второй вариант – оптимум близко. Здесь возможны три решения: окончание исследования; переход к планам второго порядка (для построения модели в виде полинома второго порядка); движение по градиенту. Переход к планированию второго порядка позволяет с высокой точностью описать область оптимума (так называемую «почти стационарную область») и найти экстремум.
Движение по градиенту следует использовать только в случае малой погрешности опытов, так как наличие большой погрешности затрудняет определение малых приращений параметра оптимизации.
2.4.1.8 Линейная модель неадекватна. Неадекватность линейной модели означает, что аппроксимировать поверхность отклика плоскостью не удалось. Мероприятия, которые можно осуществить для получения адекватной модели: изменение интервалов варьирования факторов; перенос центра плана (основного уровня); достройка плана.
2.4.1.9 Модель в
виде неполного квадратного уравнения может быть адекватна и неадекватна. В
первом случае, если область оптимума близка, то принимается решение об
окончании исследования или перехода к построению плана второго порядка.
Реализовав такой план, можно описать поверхность отклика в области оптимума с
помощью полного полинома второго порядка, включающего квадратичные эффекты
факторов, т.е. члены вида ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.