Планирование экстремальных экспериментов при оптимизации технологических процессов РЕА, страница 7

2.2.1 Основные определения

Итак, для создания полиноминальной модели ТП представляется в виде «черного ящика» ( рис. 2.1), который содержит входные параметры:

 

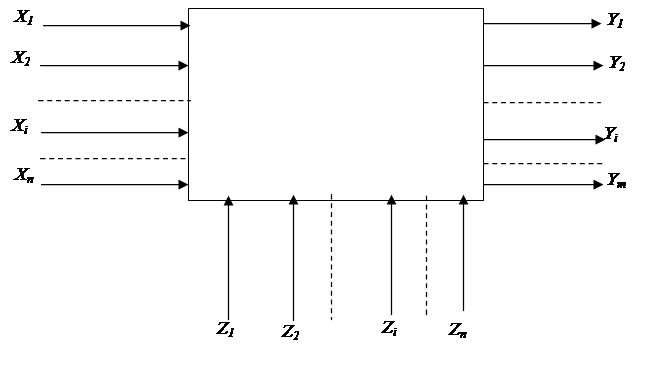Рис.2.1

 (хi и  zi ), называемые факторами, и выходные параметры (уi), называемые эффектами или функциями отклика.

Факторы хi, - например, при литье под давлением: состав сплава, давление в литьевой форме, температура металла и разогрева формы; в процессах токарной обработки; форма и размеры заготовок материала, скорость вращения заготовки, глубина резания и скорость подачи резца; в процессах намотки катушек: натяг провода, скорость намотки, отклонения диаметра провода и толщины изоляции и т.д.

Факторы zi – это нерегулируемые независимые переменные, которые также оказывают влияние на ТП. Например, температура , влажность окружающей среды в рабочей зоне, химический состав исходных материалов и т.д.

уi – параметры изделия, которые получаются в результате ТП. К ним относятся, например, геометрические размеры изделия, его точностные характеристики, шероховатость поверхности, сопротивление, индуктивность, коэффициент усиления усилителя, добротность, производительность, себестоимость и т.д. В общем случае эффекты –то это случайные величины, так как их значения зависят от факторов.

Поэтому уiпринимают как математическое ожидание параметра изделия.

Полиноминальные модели  создаются на основании экспериментальных данных, полученных при различных знвчениях (или различных уровнях) факторов, и фиксируют при этом значение эффектов, т.е. контролируемые параметры изделия. Фиксированный набор уровней факторов определяет одно из возможных опытов. Если перебрать все возможные наборы, то получают полное множество различных состояний данного ТП. Одновременно это будет количество возможных различных опытов. Если каждый из “К” факторов имеет одно и то же число уровней Р, то количество  различных опытов будет равно Р . Реализовав все эти опыты, выбирают тот из них, в котором получено наилучшее значение параметра изделия – параметра оптимизации.

2.3 Регрессионный анализ технологических процессов

Полиноминальная модель ТП получается на основании использования законов регреессионного анализа, которые предполагают, что значение зависимой переменной – параметров изделия –у ; у  и т.д. представляют собой независимые, нормально распределенные случайные величины; ошибка независимого переменного – параметров ТП - х, х и т.д. пренебрежимо мала по сравнению с ошибкой зависимого переменного; дисперсии зависимой переменной при переходе от опыта к опыту однородны. В этих условиях оценки коэффициентов регрессии будут:

-  достоверными, т.е. при увеличении объема выборки они приближаются к истинному значению параметра;

          -         несмещенными, т.е. их математическое ожидание равно оцениваемому параметру;

-       эффективными, т.е. они характеризуются минимальной дисперсией;

-   достаточными, т.е. они включают максимум информации о параметре.

          Итак, в общем случае полиноминальную модель можно представить полиномом вида:

                    y=b+  b x + b xx+  bx +…,     (2.1)

где  у – параметр изделия; b, b , b , b - коэффициенты регрессии, которые вычисляются по экспериментальным данным ( измеренные параметры изделия), x , x- управляемые независимые параметры, k– число независимых переменных.

Пусть ТП описывается полиномом

                                                     у=b+bx(2.2)

В этом случае для создания полиноминальной модели ТП необходимо определить коэффициенты регрессии b и  b.

Для этого осуществляется эксперимент, который включает измерение определяющего параметра изделия у при различных значениях параметра режима ТП х, табл.2.2.

Таблица 2.2

Номер опыта параметр	1	2	3
х	х	х	х
у	у, у, у… у	у, у, … у	у, у, … у