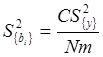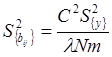Планирование экстремальных экспериментов при оптимизации технологических процессов РЕА, страница 20

                                            ,                    ;                                      (2.35)

          для коэффициентов при квадратичных членах:

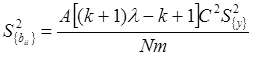                                                ;                                                 (2.36)

          для свободного члена:

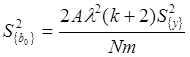
                                                       ,                                                 (2.37)

где - дисперсия воспроизводимости, вычисляемая по формуле (2.19); m – число параллельных опытов (одинаковое для каждой строки матрицы). При определении величины t для какого – либо коэффициента в знаменатель выражения (2.21) следует подставлять корень из дисперсии, соответствующий этому коэффициенту. Члены с незначимыми коэффициентами из полинома исключают.

          Адекватность полученной модели проверяется с помощью F –критерия Фишера.

2.4.4  Определение оптимальных условий реализации технологического процесса

          Точка совместной области определения факторов, в которой (в точке) параметр оптимизации имеет наилучшее значение, может являться, а может и не являться точкой экстремума функции отклика. В последнем случае крутое восхождение осуществляется до тех пор , пока это позволяют возможности технологического процесса. Наилучшая точка будет располагаться на границе совместной области определения факторов.

          Если функция отклика в совместной области определения факторов имеет точку экстремума, то целесообразно найти ее точные координаты. Для этого функция отклика в области оптимума аппроксимируется  полиномом второго порядка с включением квадратичных членов. Затем находятся и приравниваются нулю частные производные функции отклика по всем переменным (факторам)

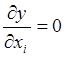                                              ,                  i = 1,2,…,к.

          Решая полученную систему уравнений, определяют координаты точки экстремума. Найденные значения факторов и будут являться оптимальными условиями реализации технологического процесса.

ЛИТЕРАТУРА

1.  Адлер Ю. П., Маркова Е. В., Грановский Ю. В. Планирование эксперимента при поиске оптимальных условий. – М.: Наука, 1976. – 280 с.

2.  Глудкин О. П., Обичкин Ю. Г., Блохин В. Г. Статистические методы в технологии производства радиоэлектронной аппаратуры. – М.: Энергия, 1977. – 296 с.

3.  Налимов В. В., Чернова Н. А. Статистические методы планирования экстремальных экспериментов. – М.: Наука, 1965. – 340 с.

4.  Букшан В. Д., Долгов Ю. А., Олейник Т. В. и др. Оптимизация технологического процесса травления печатных плат и регенерации травящего раствора. – Средства связи. 1979, вып. 4, с 32 – 34.

5.  Бусленко Н. П. Математическое моделирование производственных процессов на цифровых вычислительных машинах. – М.: Наука, 1964. – 362 с.

6.  Грановский Ю. В. Основы планирования экстремального эксперимента для оптимизации многофакторных технологических процессов. – М.: Московский институт народного хозяйства, 1971. – 72 с. ил.

7.  Душинский В. В., Пуховский Е. С., Радченко С. Г. Оптимизация технологических процессов в машиностроении. – Киев: Техника, 1977. – 176 с. ил.

8.  Современные методы исследования многофакторных технологических процессов: Методическая разработка по проведению практических занятий. – Л.: Ленинградский институт авиационного приборостроения, 1976. – 57 с. ил.

9.  Тявловский М. Д., Хмыль А. А., Станишевский В. К. Технология деталей и периферийных устройств ЭВА. – Минск: Высшая школа, 1981. – 256 с.

10.Буловский П. И., Миронов В. М. Технология радиоэлектронного аппаратостроения. – М.: Энергия, 1971. – 344 с.

11.Болтянский В. Г. Оптимальное управление дискретными системами. – М.: Наука, 1973. –  447 с.

12.Ланге О. Оптимальные решения – М.: Прогресс, 1967. – 285 с.

13.Спиридонов А. А. Планирование эксперимента при исследовании технологических процессов. – М.: Машиностроение, 1981. – 184 с.