Планирование экстремальных экспериментов при оптимизации технологических процессов РЕА, страница 18

          В качестве примера в табл.2.7 приведена матрица ортогонального ЦКП для двух факторов.

Таблица 2.7

          Реализация матрицы ортогонального ЦКП проводится в соответствии с п. 2.4.1.4.

          Коэффициенты полинома при взаимодействиях и факторах определяются по формулам: 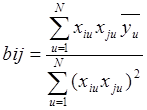   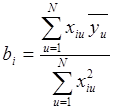                ;                          .                         (2.25)

          Коэффициенты при квадратичных членах определяются по формуле

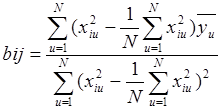                                       .                                                    (2.26)

          Свободный член определяется по формуле

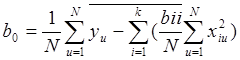                                        .                                                       (2.27)

          Процедура проверки значимости полученных коэффициентов аналогична описанной в п.2.4.1.5 за исключением пункта, касающегося вычисления оценки дисперсии этих коэффициентов. При реализации ортогональных ЦКП коэффициенты полинома определяются с неодинаковыми дисперсиями, которые рассчитываются по формулам:

          для коэффициентов при факторах и взаимодействиях:

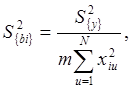
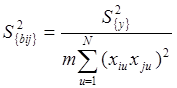                                                           ;                          (2.28)

          для коэффициентов при квадратичных членах:   

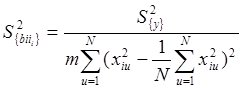                                               ;                                                (2.29)

          для свободного члена

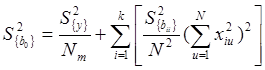                                               ,                                               (2.30)

где - дисперсия воспроизводимости, вычисляемая по формуле (2.19); m –число параллельных опытов (одинаковое для каждой строки матрицы). При определении величины t для какого-либо коэффициента в знаменатель выражения (2.21) следует подставлять корень из дисперсии, соответствующей этому коэффициенту.

          После исключения членов полинома с незначимыми коэффициентами проверяют адекватность полученной модели. Процедура проверки аналогична описанной в п.2.4.1.5.

          2.4.3 Построение модели с использованием ротатабельного ЦКП