Планирование экстремальных экспериментов при оптимизации технологических процессов РЕА, страница 12

          Следует подчеркнуть, что столбцы факторов в матрице служат для непосредственного определения условий опытов и расчета оценок коэффициентов регрессии, а столбцы взаимодействий и фиктивной переменной – только для расчета оценок коэффициентов регрессии. Указанные оценки для коэффициентов регрессии при факторах и фиктивной переменной вычисляются по формуле

                                                       ,

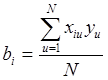где N – число опытов в матрице; i= 0,1,…,k..

например, для оценки коэффициента регрессии при факторе х1 табл.2.3 получим

.

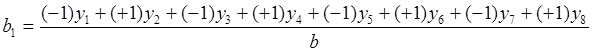Оценки коэффициентов регрессии при взаимодействиях вычисляются аналогично, т.е. в каждом опыте значения параметра оптимизации и соответствующего взаимодействия перемножаются, полученные произведения складываются, и сумма делится на число опытов в матрице.

          При большом количестве факторов к реализация ПФЭ вызывает затруднения, так как число опытов N=2, как было указано выше, сильно возрастает.

          2.4.1.3 Планирование дробного факторного эксперимента

          Вообще говоря, для определения направления градиента в исходной точке достаточно иметь модель в виде линейного полинома

.

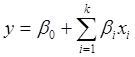Число опытов, необходимых для оценки коэффициентов регрессии в такой модели, оказывается значительно меньше, чем в ПФЭ.

          Однако, если поверхность отклика обладает существенной кривизной, то линейная модель, используемая для аппроксимации функции отклика вблизи исходной точки, может оказаться неадекватной. Это означает, что предсказанные по модели значения параметра оптимизации будут отличаться от фактических больше, чем на некоторую заранее заданную величину.

          При оптимизации технологических процессов постулируется, что функция отклика является аналитической. В случае путем уменьшения размеров области, в которой строится математическая модель, т.е. путем уменьшения интервалов варьирования факторов всегда можно добиться того, что линейная модель станет адекватной. Следует, однако, помнить о том, что ширина интервалов варьирования ограничена по минимуму из-за наличия погрешностей задания факторов при осуществлении технологического процесса.

          Таким образом, полагая, что поверхность отклика не имеет существенной кривизны, мы можем начать с построения линейной модели. Если она окажется адекватной, то ее можно использовать для нахождения направления градиента функции отклика. Если модель неадекватна, то возможны два решения. Первое состоит в уменьшении интервалов варьирования факторов и повторении эксперимента. Второе заключается в реализации ПФЭ, т.е. в постановке дополнительных опытов для получения модели в виде неполного квадратного уравнения, в котором нелинейность поверхности отклика описывается эффектами взаимодействия.

          Для построения линейной модели при большом количестве факторов используется дробный факторный эксперимент (ДФЭ), который реализует часть (дробную реплику) ПФЭ.

          Запишем матрицу планирования для ПФЭ типа 2, табл.2.4.

Таблица 2.4

          Пользуясь таким планированием, можно представить результаты эксперимента в виде неполного квадратного уравнения

.

          Если имеются основания считать, что при выбранных интервалах варьирования процесс может быть описан линейной моделью, то  и столбец х1х2 можно использовать для нового фактора х3 (в матрице планирования этот фактор стоит в скобках над взаимодействием х1х2). Изменяя х3 в процессе эксперимента согласно столбцу х1х2. Найдем