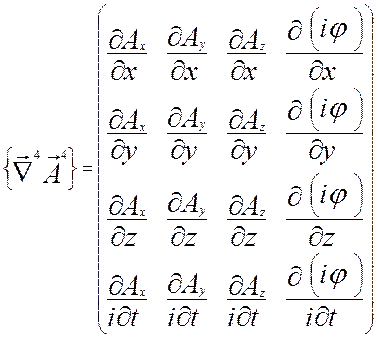 .
.
Соответствующий этому тензору антисимметричный тензор Aμν, найденный по правилу II, запишется следующим образом:
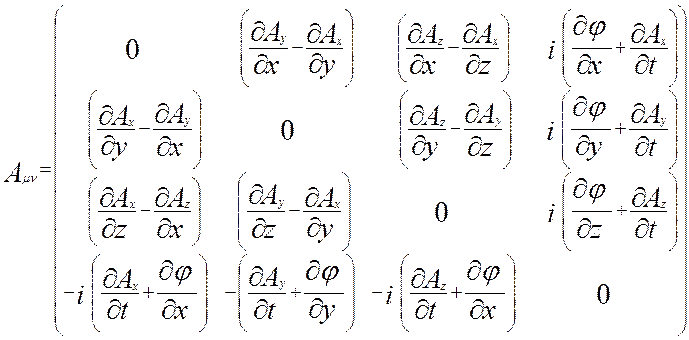 .
.
Видно, что в скобкахAμν стоят компоненты векторов магнитного и электрического полей (см. соотношение 1.3.2):
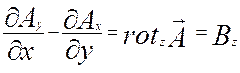 и т.д., а
и т.д., а
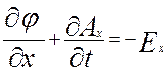 и т.д.
и т.д.
Окончательно, антисимметричный тензор второго ранга Aμν включает в себя все проекции векторов электрического и магнитного поля в качестве компонент. Поэтому он называется тензором электромагнитного поля:
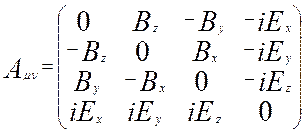 . (1.3.3)
. (1.3.3)
Из записи тензора видно, что его компонентами являются проекции векторов, обозначаемых с помощью одного индекса проекции. Поэтому векторные величины также называют тензорами, но тензорами первого ранга. Следуя этой логике, скалярные величины называют тензорами нулевого ранга.
Возвращаясь к явлению теплопроводности, с которого начато знакомство с тензорами, запишем тензор теплопроводности в общем виде:
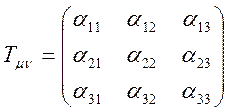 . Эксперимент
показывает, что теплопроводность характеризуется одинаковыми параметрами:
скорости процесса в прямом и обратном направлении по величине совпадают.
Наблюдается центральная симметрия. Следовательно, Тμν
должен быть симметричным тензором, у которого αij = αij.
Для симметричного тензора второго ранга возможно не только аналитическое, но и
наглядное геометрическое представление в виде поверхности второго порядка.
Действительно, с помощью компонент тензора можно записать выражение:
. Эксперимент
показывает, что теплопроводность характеризуется одинаковыми параметрами:
скорости процесса в прямом и обратном направлении по величине совпадают.
Наблюдается центральная симметрия. Следовательно, Тμν
должен быть симметричным тензором, у которого αij = αij.
Для симметричного тензора второго ранга возможно не только аналитическое, но и
наглядное геометрическое представление в виде поверхности второго порядка.
Действительно, с помощью компонент тензора можно записать выражение:
α11x2 + α22y2 + α33z2+ 2α12xy +2α13xz +2α23yz =1.
При положительных коэффициентах это уравнение в трехмерной ортогональной системе координат характеризует эллипсоид (рис. 2’).
 |
Рис.2’. Характеристическая поверхность симметричного тензора
второго ранга
Полученная геометрическая фигура имеет и свою собственную ортогональную систему координат (x’,y’,z’), оси которой являются продолжениями главных полуосей эллипсоида. В новой системе координат аналитическая запись поверхности эллипсоида упростится:
![]() α’11(x’)2
+ α’22(y’)2 + α’33(z’)2
= 1.
α’11(x’)2
+ α’22(y’)2 + α’33(z’)2
= 1.
![]()
Соответственно, проще будет запись тензора теплопроводности:
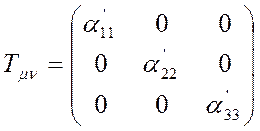 .
.
Очевидно, что в сечении эллипсоида оказывается эллипс, а это как раз та форма, которая характеризует эксперимент (рис. 2) по теплопроводности в анизотропной среде. Таким образом, применяемый математический аппарат адекватно отражает рассматриваемое явление.
§ 4. ЭЛЕКТРОМАГНИТНАЯ ВОЛНА И ЕЕ ХАРАКТЕРИСТИКИ.
Как было выяснено в §2, векторная модель электромагнтного поля позволяет дать описание основных экспериментальных фактов, связанных с объединением электрических и магнитных явлений в единую теорию (теорию Максвелла). Основные положения теории укладываются в систему дифференциальных уравнений Максвелла – Герца.
1. Вихревое магнитное поле в каждой точке пространства определяется токами проводимости и смещения (меняющимся во времени вектором индукции электрического поля) в этой же точке:
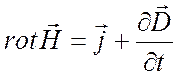 .
.
2. Вихревое электрическое поле в каждой точке пространства определяется меняющимся во времени вектором индукции магнитного поля в этой же точке:
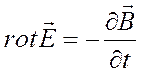 .
.
3. Источником расходимости электрического поля в каждой точке пространства является наличие в ней источника (заряда) с плотностью ρ :
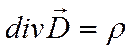 .
.
4. Ни в одной точке пространства магнитное поле не имеет источников расходимости:
![]() .
.
Часто используются в расчетах дополнительные соотношения, связывающие между собой отдельные параметры поля:
(а). Материальные соотношения: ![]() ;
;
(б). Закон Ома и уравнение непрерывности линий тока в проводнике:
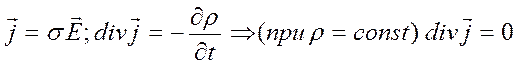 .
.
В однородной среде величины электрической и магнитной проницаемости, а также удельная проводимость постоянны (ε = const, μ = const, σ = const), поэтому учитывая материальные соотношения, уравнения Максвелла принимают вид:
1. 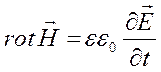 , 2.
, 2. 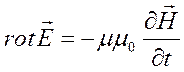 , 3.
, 3. ![]() , 4.
, 4. ![]() . (1.4.1)
. (1.4.1)
Применение к полученной системе уравнений одной из
дифференциальных операций второго порядка (двойной операции ротора), позволяет
разделить переменные ![]() и
и ![]() , затем
приводит к двум независимым уравнениям, определяющим поведение электрического и
магнитного полей в пространстве и времени:
, затем
приводит к двум независимым уравнениям, определяющим поведение электрического и
магнитного полей в пространстве и времени:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.