Радиофизические методы дистанционного зондирования земли, страница 5

В основе наших знаний о геофизических процессах на Земле лежит интуиция и опыт дистанционного зондирования в оптическом диапазоне. Только в последние два десятилетия мы стали "видеть" синоптическую картину Земли в других частях спектра электромагнитных волн и смогли оценить возможности СВЧ-диапазона по сравнению с видимым и инфракрасным.

Россия имеет многолетний опыт создания и эксплуатации космических средств. Успешно эксплуатируется оперативная  метеорологическая сеть космических аппаратов серии «Метеор», спутников «Метеор-Природа». Используется информация оперативного наблюдения суши космическими аппаратами «Ресурс – 01» и океана «Океан – 01». Фотокартографирование производится аппаратами серии «Ресурс – Ф» и спутниками двойного назначения.

С помощью метода дистанционного зондирования решается широкий круг экономических и научных задач мониторинга природной среды. Ими являются:

·  контроль погодообразующих и климатообразующих факторов;

·  контроль за состоянием источников загрязнения атмосферы, воды и почвы;

·  оперативный контроль чрезвычайных ситуаций техногенного и природного характера;

·  информационное обеспечение решений рационального землепользования;

·  создание динамической модели Земли как системы – среды обитания человека.

Рис.1. Признаки цивилизации на континентах Европы и Азии

Достаточно даже обычных  ночных фотографий земных континентов, полученных из космоса (рис.1, оптический диапазон), как  появляется объективная информация о потреблении энергии того или иного государства. Можно говорить о «признаках цивилизации» на континенте. Зондирование Земли с использованием всего спектра электромагнитных излучений, естественно даст гораздо больше информации, чем один оптический диапазон, тем более, что круг практических применений радиочастот для целей зондирования, последнее время резко возрастает. 

ЧАСТЬ I.  МОДЕЛИ ЭЛЕКТРОМАГНИТНОГО  ПОЛЯ

§ 1. Основные понятия в математической модели поля.

При моделировании физических процессов и описании физических объектов используются математические методы, в основе которых лежит понятие математической величины как меры определенного физического свойства. Если каждой точке Р пространства V (или некоторой его части) поставить в соответствие определенное значение некоторой величины, то говорят, что в V определено п о л е   этой величины. В зависимости от рода величины можно говорить о скалярном, векторном или тензорном поле.

 Для определенности описания реальное трехмерное пространство обычно относится к некоторой системе координат (например, декартовой), в которой задание точки P_i равносильно заданию ее координат x_i, y_i, z_i в этой системе, а функция физической величины поля u(P) превращается в обычную функцию трех переменных u(x,y,z). Выбор системы координат обычно связан с симметрией описываемого объекта или определен условиями, в которых находится исследуемый объект. Часто используемыми системами координат являются ортогональные системы, в которых единичные орты в каждой точке образуют правую тройку векторов e_i (i = 1, 2, 3), отношение между которыми определяется скалярными произведениями вида: (e_i, e_j) = 0 и         (e_i, e_i) = 1. 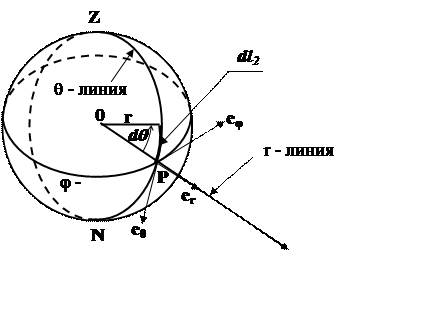Примерами ортогональных систем координат являются: декартова, цилиндрическая и сферическая, последовательность записи координат в которых (q₁, q₂, q₃) соответственно производится следующим образом:          (x, y, z); (r, φ, z) и (r, θ, φ).

Рис. 1. Координатные линии в сферической системе координат