Радиофизические методы дистанционного зондирования земли, страница 8

Поэтому описание теплопроводности с помощью векторов, однозначно определенных в каждой точке анизотропной среды, становится невозможным и требуется другой (тензорный) подход.

Вначале рассмотрим, каким образом вводится тензорная величина для характеристики другого явления, также хорошо известного из программы школьного курса физики – поляризации диэлектрика. Суть явления заключается в том, что под действием внешнего электрического поля в диэлектрике возникает поле поляризацииза счет ориентации молекулярных диполей внешним полем. В простейшем случае изотропной среды диэлектрика поле поляризациипропорционально внешнему полю, где величина α характеризует поляризуемость диэлектрика (рис. 3а).

, ,.

Если поляризуемость диэлектрика в разных направлениях различна, то произвольно направленное поле можно разложить по направлениям осей координат и записать поле поляризации также в проекции на выбранные координатные направления (рис. 3б).

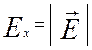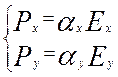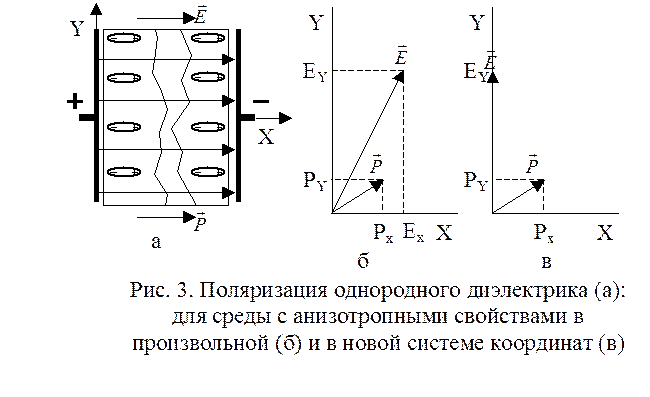
, где , , т.к. поле поляризации обычно не превышает внешнего поля. Из рис. 3б видно, что направления векторов и не совпадают. Совместим теперь внешнее поле с осью Оy. Тогда E = E_y, E_x = 0. Если среда анизотропна, то опять вектор не будет совпадать с . Это изображено на    рис. 3в. Поле вектора поляризации характеризуется проекциями, не равными нулю.

Тогда P_y = α_yE_y и P_x = α_xyE_y, где α_xy характеризует поляризуемость диэлектрика в направлении Оx, когда поле направлено по оси Oy. Наконец, нетрудно перейти к общему соотношению для P_x и P_y в зависимости от E_x и E_y, когда ипроизвольны:

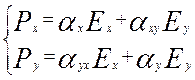 или 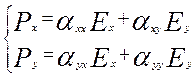, где α_x обозначено как α_xx, а α_y – как α_yy. В трехмерном случае связь между и следует записать уже в виде трех уравнений:

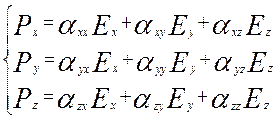, что формально можно представить следующим образом:

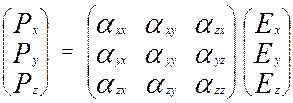
или еще короче , где величина 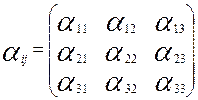, характеризующая поляризуемость диэлектрика по различным направлениям, и называется тензором поляризуемости. Так как для его записи оказалось достаточно использовать пару индексов, то в математике α_ij называется тензором второго ранга. Рассмотрим их некоторые свойства.

Тензоры  и 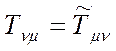 отличаются друг от друга заменой строк на столбцы и называются транспонированными по отношению друг к другу. Если компоненты тензора  для всех индексов, то такой тензор  называется симметричным, а если , то  – антисимметричный. Легко доказать, что любой тензор  можно разбить на сумму, а  – на разность симметричного и антисимметричного тензоров (складываются и вычитаются при этом компоненты тензоров  или ). Симметричный тензор  строится из  по правилу (I): 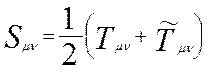 ,  а антисимметричный – по правилу (II):       .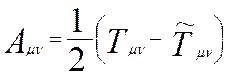

Представим далее электромагнитное поле в тензорной форме в четырехмерном пространстве событий, в котором радиус-вектор точки фиксируется тремя пространственными координатами (x, y, z) и моментом времени t. Вводя четвертую координату ict = x₀ и обозначая x = x₁, y = x₂,    z = x₃, запишем оператор набла как четырехмерный вектор: .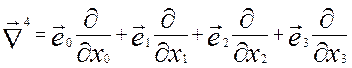

Для удобства расчетов в теории выбирается такая система единиц, в которой скорость света в вакууме c принимается за единицу, т.е. x₀ = it. Тогда в четырехмерной декартовой системе координат оператор набла можно записать следующим образом: 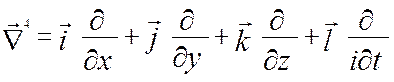.  Как было сказано в конце предыдущего параграфа, электромагнитное поле в вакууме допускает два альтернативных представления: либо с помощью векторов электрического и магнитного поля  и и  уравнений

Максвелла: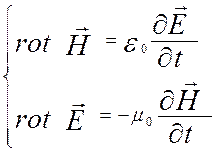 ,                                              (1.3.1)  либо с помощью потенциалов: скалярного φ и векторного , причем переход от одного способа описания к другому определяется соотношениями

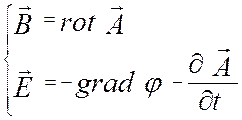 ,                                                                 (1.3.2)

откуда видно, что векторный потенциал определяет магнитное поле, а скалярный и меняющийся во времени векторный потенциал определяют электрическое поле. Образуем из скалярного и векторного потенциалов четырехмерный вектор 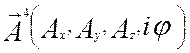, который становится основной векторной характеристикой электромагнитного поля. Кроме этого, форма поля характеризуется градиентом потенциала, поэтому составим тензорное (смешанное) произведение в четырехмерном пространстве вектора градиента и потенциала: