Радиофизические методы дистанционного зондирования земли, страница 15

1.  Расшифровка структур по дифракционной картине.

Пусть объект представляет собой некоторую простую двумерную структуру из рассеивающих точек - атомов, которая аппроксимируется функцией рассеяния f(x,y) (рис. 7а). Соответствующий полевой образ структуры будет определяться амплитудами рассеянных волн F(h,k), то есть можно записать . Детекторы, регистрирующие рассеянные волны являются «квадратичными», так как они способны производить лишь запись величины энергии, пропорциональной квадрату волны |F(h,k)|². Используя теорему о свертке, составим произведение образов прямой (рис.7а) и инвертированной (рис.7б) структур:

, а затем произведем обратное преобразование Фурье от функции |F(h,k)|² , что позволит перейти к координатному пространству (x,y):

.

Учитывая, что свертка «размножает» точки одной структуры по точкам другой, в реальном пространстве получаем «квадратизированную» структуру (рис. 7в), по которой специальными методами (например, методом сдвига начала диаграммы функции в другие точки диаграммы) удается определить либо исходную, либо инвертированную структуру. Подробности расшифровки конкретных кристаллических структур можно найти в учебной и научной литературе по кристаллографии и рентгеновскому структурному анализу.

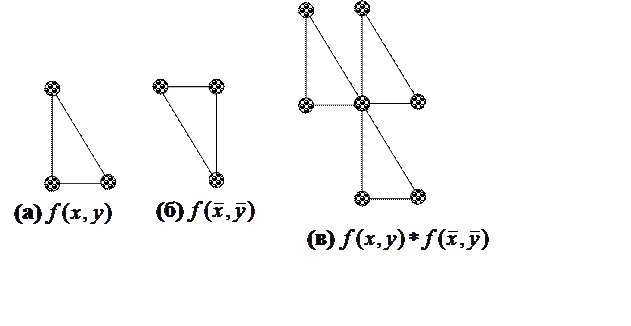Рис. 7. Определение структуры по свертке

Несмотря на то, что исторически, на начальном этапе использования ЭМВ способы определения структур базировались на оптическом и рентгеновском диапазоне, весь математический аппарат применяется и в настоящее время без изменений для обработки результатов зондирования реальных объектов ИК- и радиочастотными методами.

2.  Фильтрация изображений.

Допустим, что произведена одновременная запись изображения от двух объектов, которые описываются в пространстве функциями рассеяния f(x,y,z) и t(x,y,z). Общая картина рассеяния при этом будет определяться сверткой этих функций , а в пространстве будет зафиксирован образ G(h,k,l) = F(h,k,l)∙T(h,k,l)=F∙T. Чтобы «восстановить» или, другими словами, выделить «объект f(x,y,z)» на общем фоне, необходимо «приготовить» фильтр (φ). Для этого фиксируем образ инвертированного второго объекта , вид которого известен. Математически эта процедура записывается следующим образом: . Затем отдельно фиксируем квадратизированный образ этой же функции: 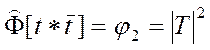, а затем из полученного «негатива» делаем «позитив». В результате фиксированная функция станет обратной: 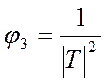. Совместное пропускание наложенных друг на друга фильтров  φ₁ и φ₃ приведет к результирующему фильтру φ :

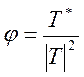, который, в свою очередь, накладывается на исходное изображение G(h,k,l). Пропускание  φ∙G даст «на выходе» образ искомого объекта: 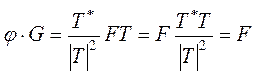. Используя собирающую линзу, произведем обратное преобразование Фурье и восстановим изображение реального объекта. Все этапы производства фильтров после «оцифровки» исходной фотографии и известного объекта (t(x,y,z)) можно провести с помощью компьютера, используя современные математические комплексы программ.

3.  Основы голографии.

Не нарушая общности анализа основ голографии, представим метод в оптическом диапазоне ЭМВ. Слово – голография – произошло от двух корней: голос, по-гречески означает «полный» или «весь», и графо – «пишу». Таким образом метод предполагает полную запись и восстановление трехмерного изображения объектов (нобелевская премия Денеша Габора 1960года). Простейшая схема голографии «на встречных пучках» с использованием ОКГ (рис. 8) была предложена Ю.Н.Денисюком и позволяет получать при наличии высокоразрешающих фотоматериалов (записывающих до 6000 штрихов/мм) качественные трехмерные изображения реальных объектов. Метод основан на интерференции волн, идущих от объекта и от оптического квантового генератора (лазера).

Введем обозначения:

U₁=U₀e^iφo - волна, идущая от источника к фотопластинке;

U₂=U₀e^iφ - волна, идущая от предмета к фотопластинке;