Радиофизические методы дистанционного зондирования земли, страница 13

При сложении большого количества волн с частотами, укладывающимися в некоторой полосе частот ∆f   (ω=2πf ), сигнал принимает форму волнового пакета (рис. 5б) и его распространение можно охарактеризовать двумя скоростями: фазовой (u_ф), с которой распространяется в пространстве фиксированная фаза каждой из составляющих группу волн и групповой (u_гр) скоростью, с которой распространяется максимум волнового пакета, его амплитуда . Тогда формально определение этих скоростей может быть записано следующим образом:

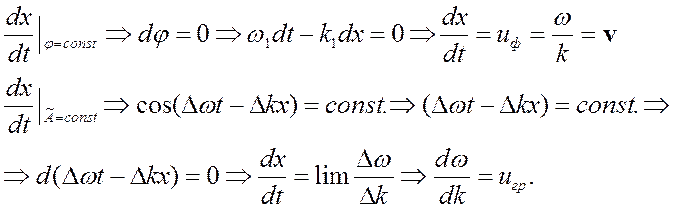    (1.7.1)

Из формул (1.7.1) видно, что групповая и фазовая скорости не одинаковы, а фазовая скорость совпадает с обычной скоростью волны (1.5.3). В среде из-за явления дисперсии фазовые скорости различных составляющих сигнала отличаются друг от друга и поэтому волновой пакет начинает «расползаться» так, как это происходит с группой бегунов, постепенно удаляющихся друг от друга на дистанции. Соотношение между групповой и фазовой скоростью легко рассчитать, исходя из полученных формул (1.7.1).

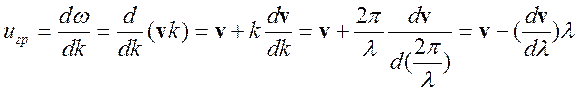.               (1.7.2)

Это соотношение (1.7.2) носит название: формула Рэлея.

При освещении объекта электромагнитной волной, по принципу Гюйгенса – Френеля, каждая точка объекта с координатой x становиться источником вторичных волн: модулирует интенсивность падающей волны в соответствии со своей рассеивающей способностью ρ(x_j) и меняет фазу волны в соответствии с координатой. В пространстве распространяется вторичная волна, которая после усреднения амплитуды по времени может быть записана следующим образом: 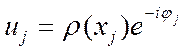. Если, для определенности, в качестве объекта избрать дифракционную решетку, то в пространстве образуется дифракционная картина, порядки дифракции которой h, заданные направляющими косинусами в фиксированной системе координат, будут характеризоваться интенсивностями, полученными в результате сложения волн от точек дифракционной решетки. Тогда можно записать следующее выражение:

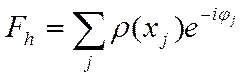.                                                             (1.7.3)

Если теперь на пути рассеянных волн с амплитудами F_h поставить собирающую линзу или любым другим способом (в том числе и математически) собрать (сложить) эти рассеянные волны, то мы снова получим образ объекта ρ(x_j) в виде распределения в пространстве рассеивающих точек:

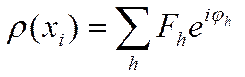 .                                                                 (1.7.4)

В общем случае, для произвольно взятого объекта величины координат и направляющих косинусов (проекций волнового вектора) меняются непрерывно, в фазу волны эти переменные входят симметрично (φ_j = φ_h=φ) , поэтому суммирование заменяется интегрированием. Выражения (1.7.3) и (1.7.4) образуют пару соотношений, которые называются преобразованиями Фурье:

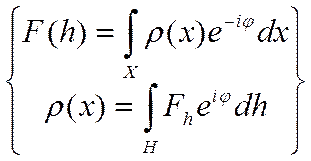 .                                                (1.7.5)

Так как экспоненциальная функция, входящая в эти преобразования может быть разложена по формуле Эйлера (см. §4), то существуют косинусовое и синусовое преобразования Фурье. Выражения (1.7.3) и (1.7.4) являются примером дискретных, а (1.7.5) примером непрерывных преобразований Фурье. Функция F(h) называется «образом» функции ρ(x). Обобщение преобразований Фурье для трехмерного пространства является чисто техническим усложнением и может быть записано следующим образом:

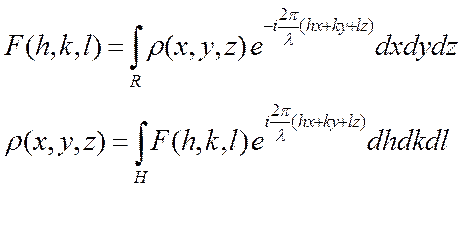   ,                              (1.7.6)

где пространство объекта R задано векторами , а пространство образов H задано волновыми векторами так называемого «обратного пространства» . Числа h,k,l иногда называют пространственными частотами. Инверсия координат в пространственной области равносильна комплексному сопряжению в обратном пространстве, так как в фазе замена переменной x на –x приводит к появлению минуса перед символом мнимой единицы:

. 

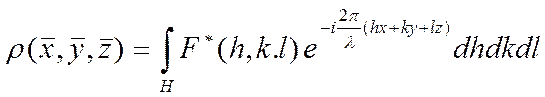Символически, после введения оператора фурье-преобразований  и обратных фурье-преобразований , формулы (7.6) можно записать следующим образом:

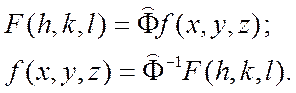                                                    (1.7.7)