С другой стороны силовая характеристика поля – его
напряженность ![]() характеризуются в геометрической
модели поля густотой силовых линий в окрестности выбранной точки. Поэтому
напряженность можно измерять количеством силовых линий, пересекающих единичную
площадку, расположенную перпендикулярно силовым линиям. Тогда величина
напряженности, как и дивергенция, определяется плотностью (поверхностной
плотностью) числа силовых линий. Следует записать
характеризуются в геометрической
модели поля густотой силовых линий в окрестности выбранной точки. Поэтому
напряженность можно измерять количеством силовых линий, пересекающих единичную
площадку, расположенную перпендикулярно силовым линиям. Тогда величина
напряженности, как и дивергенция, определяется плотностью (поверхностной
плотностью) числа силовых линий. Следует записать 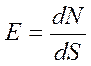 или,
учитывая направление вектора напряженности относительно нормали к площадке,
проходящей через выбранную точку,
или,
учитывая направление вектора напряженности относительно нормали к площадке,
проходящей через выбранную точку, ![]() Если сложить все
элементарные потоки через замкнутую поверхность, ограничивающую некоторый объем
V, то получаем интегральную теорему Гаусса –
Остроградского :
Если сложить все
элементарные потоки через замкнутую поверхность, ограничивающую некоторый объем
V, то получаем интегральную теорему Гаусса –
Остроградского :
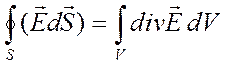 .
.
Опыты Эрстеда показали, что магнитное поле с индукцией
![]() в каждой точке пространства согласовано с
направлением электрического тока таким образом, что силовые линии вектора
в каждой точке пространства согласовано с
направлением электрического тока таким образом, что силовые линии вектора ![]() замкнуты, образуя циркуляцию вокруг тока.
Если на поверхности S выбрать произвольный контур L,
охватывающий токи, которые пересекают эту поверхность, то сумма элементов
циркуляции
замкнуты, образуя циркуляцию вокруг тока.
Если на поверхности S выбрать произвольный контур L,
охватывающий токи, которые пересекают эту поверхность, то сумма элементов
циркуляции ![]() по контуру L образует
интегральную циркуляцию
по контуру L образует
интегральную циркуляцию 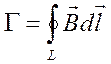 . С другой стороны,
рассматривая циркуляцию по контуру L как сумму циркуляций ΔГ
по малым контурам ΔL , образующим разбиение поверхности S на
отдельные площадки ΔS , можно ввести отношение ΔГ/ΔSдля
характеристики вихревого магнитного поля в каждой точке. Для этого перейдем к
поверхностной плотности циркуляции
. С другой стороны,
рассматривая циркуляцию по контуру L как сумму циркуляций ΔГ
по малым контурам ΔL , образующим разбиение поверхности S на
отдельные площадки ΔS , можно ввести отношение ΔГ/ΔSдля
характеристики вихревого магнитного поля в каждой точке. Для этого перейдем к
поверхностной плотности циркуляции![]() , то есть к производной
в выбранной точке и снабдим площадку dS
направлением нормали, согласованной с правилами обхода контура ΔL.
Полученная в результате величина элементарного вихря, называется ротором:
, то есть к производной
в выбранной точке и снабдим площадку dS
направлением нормали, согласованной с правилами обхода контура ΔL.
Полученная в результате величина элементарного вихря, называется ротором: 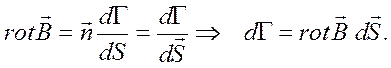 Поток ротора по поверхности S,
ограниченной контуром L, определит полную циркуляцию Г по этому контуру:
Поток ротора по поверхности S,
ограниченной контуром L, определит полную циркуляцию Г по этому контуру: 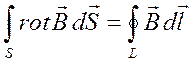 . Полученное интегральное равенство
называется формулой Стокса. Учитывая, наконец, что поток ротора
определяется потоком вектора плотности тока, можно подобрать такую систему
единиц (СИ), в которой эти величины совпадут. В этом случае имеем
. Полученное интегральное равенство
называется формулой Стокса. Учитывая, наконец, что поток ротора
определяется потоком вектора плотности тока, можно подобрать такую систему
единиц (СИ), в которой эти величины совпадут. В этом случае имеем
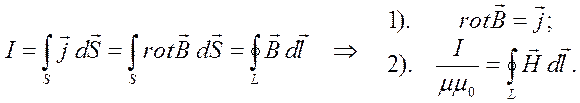
Первое
равенство входит в систему дифференциальных уравнений Максвелла для
электромагнитного поля, а второе известно как закон полного тока.
Рассмотренные выше понятия математической теории поля достаточны для
формирования векторной модели электромагнитного поля, основанной на его
описании с помощью векторов индукции магнитного поля ![]() и
напряженности электрического поля
и
напряженности электрического поля ![]() . Эта модель, как
наиболее распространенная в решении проблем зондирования, будет использована
нами на протяжении всего излагаемого материала. Тем не менее, существует
альтернативное описание электромагнитного поля с помощью потенциалов –
скалярного φ и векторного
. Эта модель, как
наиболее распространенная в решении проблем зондирования, будет использована
нами на протяжении всего излагаемого материала. Тем не менее, существует
альтернативное описание электромагнитного поля с помощью потенциалов –
скалярного φ и векторного ![]() , из
которых складывается современная тензорная модель на базе четырехмерного
векторного потенциала
, из
которых складывается современная тензорная модель на базе четырехмерного
векторного потенциала ![]() , где цифра 4 в записи потенциала
обозначает величину, представленную в четырехмерном пространстве событий.
Именно в такой форме электромагнитное поле удалось включить в единую теорию
взаимодействий (ТВО), как разновидность калибровочного поля. Поэтому кратко
рассмотрим эту модель в следующем параграфе, что позволит понять сложность
электромагнитного поля как физического объекта.
, где цифра 4 в записи потенциала
обозначает величину, представленную в четырехмерном пространстве событий.
Именно в такой форме электромагнитное поле удалось включить в единую теорию
взаимодействий (ТВО), как разновидность калибровочного поля. Поэтому кратко
рассмотрим эту модель в следующем параграфе, что позволит понять сложность
электромагнитного поля как физического объекта.
§ 3. ОСНОВНЫЕ ПОНЯТИЯ ТЕНЗОРНОЙ МОДЕЛИ.
Вначале, на примере явления поляризации диэлектриков рассмотрим условия, связанные с проявлением анизотропии, при которой возникает необходимость тензорного описания явлений.
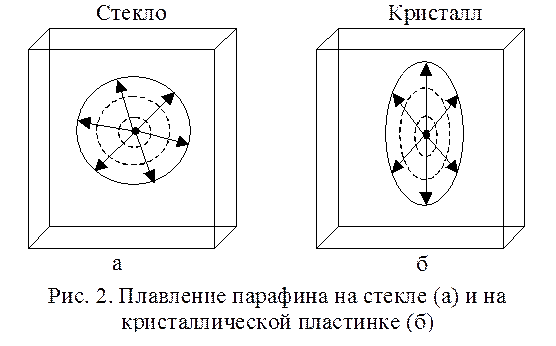 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.