Радиофизические методы дистанционного зондирования земли, страница 18

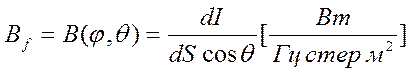4.  Спектральная яркость излучения           ,                     определяемая силой излучения единицы поверхности, перпендикулярной направлению излучения.

5.  Плотность облучения E_f(φ,θ) характеризуется спектральной мощностью ЭМВ, падающей на единицу облучаемой поверхности 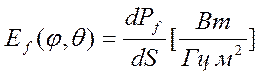 . В оптике эта величина называется освещенностью.

Найдем связь спектральной плотности мощности излучения R_f с яркостью излучения B_f . Для этого выберем объект, ограниченный гладкой поверхностью, изотропно излучающей ЭМВ по всем направлениям. Из соображений симметрии выделим внутри объекта некоторый геометрический центр, с которым свяжем сферическую систему координат. Если разбить поверхность на элементарные площадки, то каждая из них (с нормалью ) составляет определенный угол θ с зенитным направлением OZ в сферической системе координат. Тогда сила излучения dI , создаваемая проекцией элементарной площадки на зенитное направление в единичном телесном угле по определению яркости может быть найдена по формуле:

, а полная сила излучения в этом телесном угле   определится суммированием (интегрированием) этой величины по всей поверхности объекта, разбитой на элементарные площадки.

.

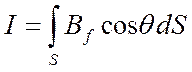Для того, чтобы вычислить спектральную мощность излучения объекта по всем направлениям, необходимо суммирование (интегрирование) по всем телесным углам, что поэтапно можно представить следующим образом:

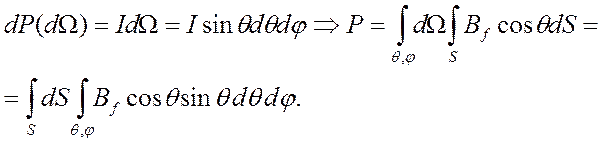
При расчете использовано определение телесного угла, бесконечно малая величина которого в сферической системе координат будет равна

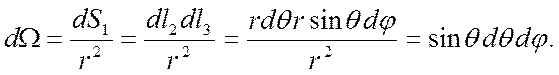
С другой стороны, спектральная мощность излучения объекта может быть вычислена через светимость (плотность излучения R_f) следующим образом:

.

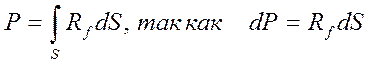Поэтому можно записать 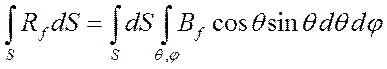 , откуда следует:

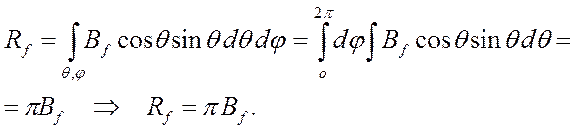
Более общий результат получиться в том случае, когда излучения площадок неизотропно и выносить яркость за пределы интегрирования не удается, так как необходимо выразить зависимость этой функции от углов в явном виде.

При пассивной локации измеряется излучение тел нагретых до физической температуры T, которая является энергетическим параметром, характеризующим тело, и ставится задача поиска соответствия между измеренной приборами  излученной энергией и истиной температурой тела. Для решения этой задачи необходимо знать законы излучения нагретых тел и связь излученной энергии с температурой. Поэтому рассмотрим кратко вывод соответствующего закона излучения на модели абсолютно черного тела (АЧТ).

§ 2. РАСПРЕДЕЛЕНИЕ ЭНЕРГИИ ПО СПЕКТРУ АЧТ. ЗАКОН ПЛАНКА И ФОРМУЛА РЭЛЕЯ.

Будем рассматривать нагретое тело, состоящее из вещества и поля, находящихся в стационарном состоянии: какое количество фотонов (квантов поля) поглощается веществом (атомно-молекулярными осцилляторами), такое же их количество переизлучается вновь, поэтому концентрация фотонов  n_γ в системе и энергия системы сохраняются с течением времени (стационарность). Распределение частиц по энергии можно найти, если знать распределение частиц по состояниям и распределение состояний по энергии. Математически это записывается следующим образом:

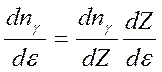 , где ε – энергия фотонов (ε = hν), обладающих импульсом 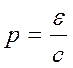  , а Z – характеризует количество состояний в фазовом пространстве координат-импульсов. Первый сомножитель, очевидно, является распределением частиц по состояниям, то есть показывает концентрацию частиц  n_γ(ν) в состоянии с энергией  ε или с частотой ν , а второй – распределением самих состояний по энергиям. Элементарная ячейка-состояние в фазовом пространстве определяется объемом               dV_ф = dxdydzdp_xdp_ydp_z ≈ h³, так как вследствие соотношения неопределенностей Гейзенберга произведения вида dx∙dp_x можно оценить не точнее, чем величина постоянной Планка h.  Если система занимает в фазовом пространстве объем V_ф = V∙V_p, где   V – объем системы в обычном, координатном пространстве, а V_p – сферический объем  в пространстве импульсов, то количество состояний Z легко определить делением фазового объема на размеры одной ячейки. Тогда для распределения состояний по энергиям, а затем и по частоте, будем иметь: