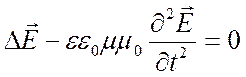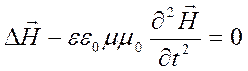Физика \ Автоматизация экспериментальных радиофизических исследований

Радиофизические методы дистанционного зондирования земли, страница 10

;

.                                                        (1.4.2)                                            

Решением этих уравнений, соответственно, являются функции вида

,

,                    (1.4.3)

которые по формуле Эйлера () легко разложить на действительную и мнимую часть, каждая из которых представляет собой периодическую функцию, являющуюся частным решением уравнения (1.4.2), что легко проверить прямой подстановкой. Если, в частном случае действительной компоненты , зафиксировать координату z (z = 0), то функция будет описывать колебания вектора напряженности в начале координат с периодом Т и частотой ω. Действительно, при t0 = 0       Δt = T  и по определению периода  ωT = 2π  , то 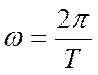 . Рассуждая аналогично, при фиксированном моменте времени (при «фотографировании» процесса), получим в пространстве периодическое распределение вектора напряженности. Величина 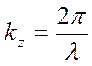  называется в данном случае волновым числом, а в общем случае одной из проекций волнового вектора  .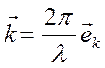

Так как процесс колебаний физической величины периодически распределенный в пространстве является определением волнового процесса, то полученные решения (1.4.3)  исходного дифференциального уравнения имеют право называться волновыми функциями, а само уравнение (1.4.2) – волновым уравнением. Таким образом, электромагнитное поле в вакууме существует в виде электромагнитной волны.

Установим соотношения между векторами в пространстве. Воспользуемся для этого третьим уравнением Максвелла (1.4.1), а также записью вектора напряженности через его проекции.

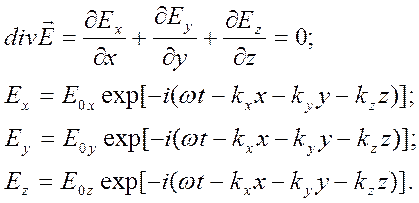                               (1.4.4)

Решая совместно систему уравнений (1.4.4), то есть после взятия производных, имеем: . Скалярное произведение векторов равно нулю, если векторы перпендикулярны. Таким же образом, получаем, что . Следовательно, , а это означает, что вектора напряженности находятся в плоскости, перпендикулярной волновому вектору. Направим волновой вектор в декартовой системе координат по оси Оz, а для вектора напряженности выберем направление по оси Oy. Тогда . О векторе напряженности магнитного поля пока можно сказать определенно только то, что его проекция  Hz= 0. Использование второго уравнения Максвелла (1.4.1) с одной стороны приводит к равенству 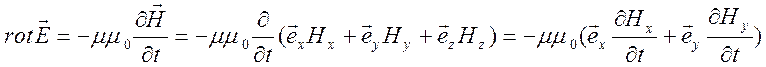, а с другой стороны, имеем:  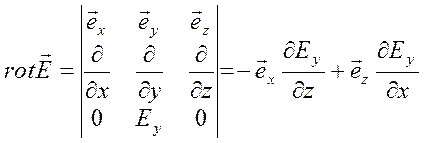. Левые части полученных уравнений одинаковы, следовательно равны и правые. Равенство векторов, в свою очередь, требует, чтобы были одинаковыми проекции при единичных векторах. Отсюда следует:

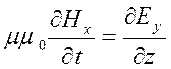.                         (1.4.5)

Очевидно, что только одна проекция Hx меняющегося магнитного поля сохраняется при фиксированных векторах и , то есть можно записать .Таким образом, все три вектора взаимно перпендикулярны.

§ 5. ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ

Симметрия электрического и магнитного полей в системе уравнений Максвелла для однородной среды (1.4.1) позволяет без расчета записать соотношение между фиксированным по оси Ox магнитным полем и получающимся в результате расчета электрическим полем, используя второе уравнение системы (1.4.1). В этом случае получим выражение

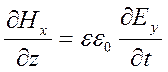.                                            (1.5.1)

Подставляя в равенства (1.4.5) и (1.5.1) выражения для проекций векторов напряженности  , получаем:

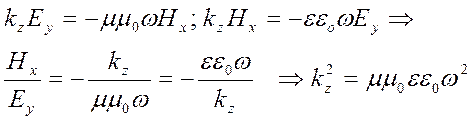.        (1.5.2)

Отношение 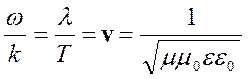.                                        (1.5.3)

Для вакуума (μ =1, ε =1) скорость распространения волны обозначается с, поэтому 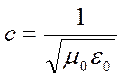  . Отношение скорости распространения волны в вакууме к скорости ее распространения в среде носит название абсолютного показателя преломления среды и легко заметить, что он зависит от свойств среды (от ε и μ) : 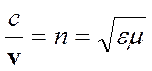. Для среды, не являющейся магнетиком (μ = 1) имеем:   и зависимость волнового числа от диэлектрических свойств среды запишется следующим образом:

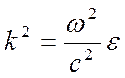 .                                                    (1.5.4)

Равенство (1.5.4) называют дисперсионным соотношением.

Для проводящей среды, содержащей свободные заряды и токи проводимости, первое уравнение Максвелла с учетом закона Ома и волновой функции вектора напряженности электрического поля (1.4.3) примет следующий вид:

Скачать файл