Радиофизические методы дистанционного зондирования земли, страница 19

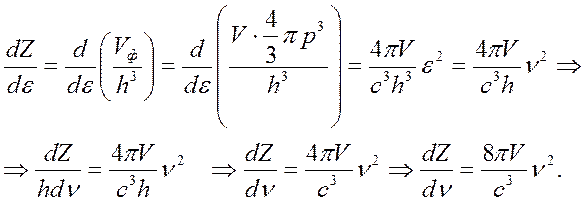
За счет поляризации (спина фотона, проекция которого принимает только два возможных значения) число состояний удваивается, что учтено в последней формуле.

С другой стороны, каждое состояние фотона с частотой ν «рождается» в процессе перехода атомно-молекулярного осциллятора из состояния с энергией Е₂ в состояние с энергией Е₁ так, что Е₂ – Е₁ = hν.

Очевидно, что равновесие в системе будет соблюдаться тогда, когда вероятность W перехода осцилляторов из первого состояния во второе будет равна вероятности обратного перехода. Условие стационарности, таким образом, будет выполнено, если  . Вероятность перехода из первого во второе состояние пропорциональна концентрации осцилляторов на первом уровне и концентрации фотонов, имеющих частоту перехода ν в системе. Следовательно, ~N₁·n_γ(ν). Обратный переход может происходить как спонтанно, самопроизвольно, так и под действием фотонов (индуцированно). Поэтому, для вероятности обратного перехода можно записать:

~N₂+N₂·n_γ(ν). Используя условие равновесия в системе, получим следующее значение для концентрации фотонов в состоянии с частотой  ν :

.

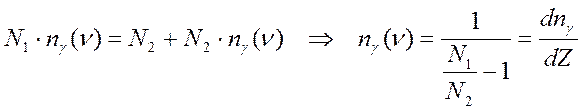Отношение «заселенности» уровней в системе рассчитывается по формуле Больцмана, справедливой не только для концентрации молекул по высоте в атмосфере: 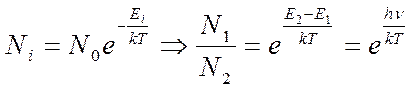. Окончательно получаем распределение фотонов по частоте:

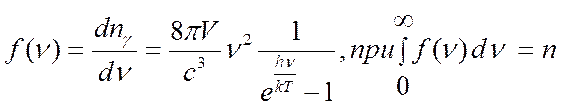.                      (2.2.1)

Переходя к концентрации (делением левой и правой части на объем V) и к отдельной частице (делением на n_γ), получаем функцию плотности вероятности по частоте, а затем и по энергии, так как ε ~ ν, а вероятность dp = dn/n :

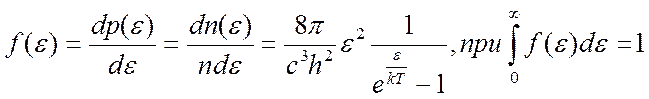.          (2.2.2)                    

Умножая полученную величину в формуле (2.2.1) на энергию отдельного фотона, и переходя к единице объема делением левой и правой части на объем, получим закон излучения Планка:

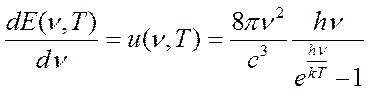. Если считать, что эта энергия излучается за единицу времени, то распределение Планка будет характеризовать спектральную плотность мощности излучения объекта из единицы объема за единицу времени. Естественно, при этом считается, что температура тела не меняется.

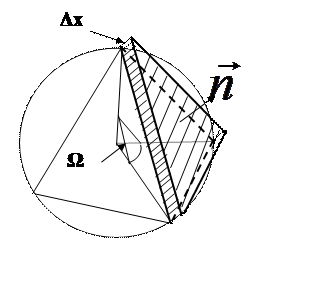
Перейдем к излучению с единицы поверхности нагретого тела и вычислим поверхностную спектральную плотность мощности R_f.  Для этого выделим в объеме тела плоскость и проследим, каким образом излучение вместе с плоскостью переходит в пространство вне тела. В качестве перемещающейся плоскости, для определенности, выберем грань объемной фигуры – тетраэдра – как полиэдра с минимальным числом граней (рис.11). Тогда в направлении нормали к грани в телесном угле Ω будет распространяться поле, составляющее четвертую часть волн, идущих наружу по всем направлениям. За малое время Δt в процессе излучения со скоростью c тело потеряет энергию, заключенную в объеме ΔV = SΔx = ScΔt . С поверхности грани за это же время произойдет излучение энергии, равной R_f SΔt . Поэтому можно записать равенство 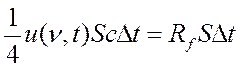, исходя из которого с учетом формулы Планка, получим:

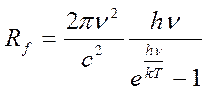                   .                                                        (2.2.3)

Рис. 11. К расчету величины поверхностной спектральной плотности мощности излучения R_f

График функции Планка (рис.12) хорошо согласуется с экспериментальной кривой по измерению спектральной плотности мощности излучения нагретых тел.   

Рис. 12. Графики функций Рэлея и Планка для R_f(ν)

Интегрирование по всем частотам спектра излучения приводит к закону Стефана – Больцмана: P(T) = σT⁴. Максимум распределения, вычисляемый по условию экстремума функции R’_f = 0, соответствует частоте, прямо пропорциональной абсолютной температуре, или соответствует длине волны, обратно пропорциональной температуре: 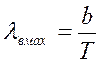 (закон «смещения» Вина). Величина постоянной Вина b =2,9∙10^-3мК может быть использована для оценки эффективности применяемой аппаратуры при локации и известных температурах источников излучения.

Если в формуле Планка (2.2.3) разложить экспоненциальную функцию  в ряд и при малых частотах  (hν << kT) ограничиться первыми двумя слагаемыми, то в результате получится функция Рэлея, выведенная им на основе не квантовых классических представлений. Действительно,