Радиофизические методы дистанционного зондирования земли, страница 6

В любой системе координат линия, вдоль которой меняется лишь одна координата, а две другие остаются постоянными, называется  l_i -координатной линией. Координатные линии в сферической системе координат показаны на рис.1. Если на второй координатной линии (θ – линии) выделить малый элемент координатной линии dl₂ , с соответствующим элементом самой координаты dθ, то связь между ними можно записать следующим образом: dl₂ = rdθ, где величина r играет роль связующего коэффициента. В общем случае произвольной криволинейной системы координат эту связь можно представить в виде dl_i = h_idq_i , где  величины h_i называются коэффициентами Ламэ. Из элементов координатных линий формируются элементарные координатные поверхности dS_i = dl_j·dl_k и элементарный объем dV = dl₁·dl₂·dl₃. В сферической системе координат коэффициенты Ламэ имеют вид: h₁= 1, h₂ = r, h₃ = rsinθ. Если рассматривать сферическую систему координат как небесную сферу, в центре которой (в точке 0) находится наблюдатель (рис. 1), то вертикальное направление вверх к точке Z называют зенитным направлением, а вниз, к точке N, надирным направлением. Оба эти понятия используются при зондировании.

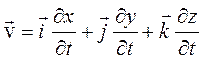Многие понятия теории векторного поля а(Р) удобно иллюстрировать на примере гидродинамического поля скоростей несжимаемой жидкости. Сравнивая запись векторов  и , представленных для простоты в декартовой системе координат, замечаем, что поля, как и течение жидкости могут быть стационарными, так и не стационарными во времени и для них можно ввести понятия векторных линий тока, потока векторных линий, их расходимости (дивергенции), циркуляции и вихря (ротора). Естественно допустить существование однородных и неоднородных полей, для которых полевые переменные либо не зависят от выбора точки (однородность), либо зависят от нее (неоднородность). В последнем случае поле в пространстве характеризуется производной по направлению или вектором градиента, определяющим крутизну поля в направлении максимального изменения его параметров. Если это направление определено, то вектор градиента потенциала поля можно представить через его проекции:

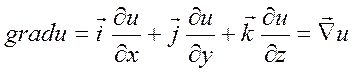, где символом введен дифференциальный оператор первого порядка – набла:

. 

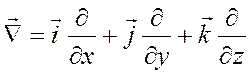Рассматривая введенный оператор как обычный вектор, перечислим все возможные операции первого и второго порядков, которые определены в курсе векторного анализа: умножение на скаляр u(P), скалярное, векторное  и смешанное умножение на вектор – функцию поля, которую для определенности обозначим так же как  вектор напряженности электрического поля . В результате, соответственно, имеем для операций дифференцирования первого порядка:

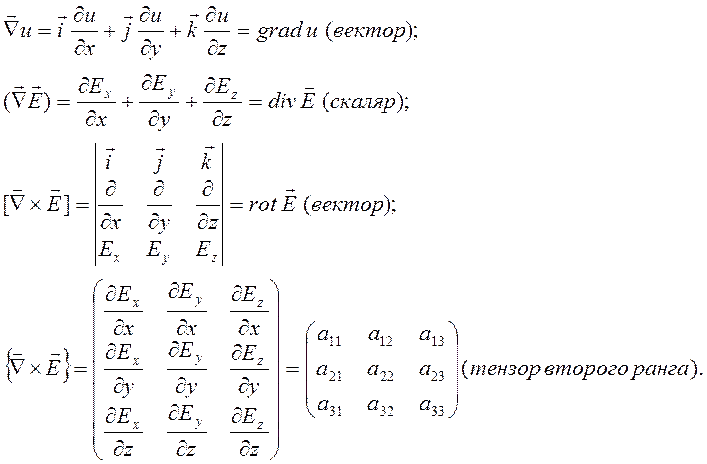(1.1.1)

Полученные скалярные и векторные величины используем еще раз совместно с оператором набла. В результате будем иметь равенства, связанные с дифференциальными операциями второго порядка:

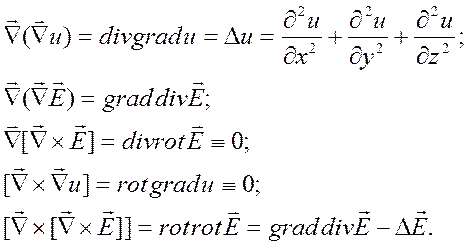                                          (1.1.2)

Введенный оператор Δ носит название оператора Лапласа.

§ 2. КЛАССИЧЕСКАЯ МОДЕЛЬ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

Представленные в равенствах (1.1.1) формальные символы дивергенции и ротора для электрического, а затем и магнитного полей, имеют со времен Фарадея наглядную геометрическую интерпретацию. Чем больше величина интенсивности поля в некоторой его точке, определяемая зарядом Q в этой точке, тем большее количество N – силовых линий необходимо использовать для изображения поля. Можно считать, что Q пропорционально N. Расходимость линий из единицы объема, то есть дивергенция по смыслу должна характеризоваться объемной плотностью числа силовых линий, то есть производной 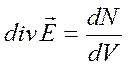  , которая в свою очередь, пропорциональна объемной плотности заряда, заключенного в этой же единице объема 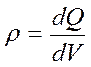. Поэтому источником расходимости силовых линий является плотность заряда в выбранной точке. В интернациональной системе единиц это утверждение выглядит следующим образом: 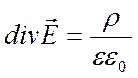, а количество силовых линий, выходящих из элементарного объема равно .