Радиофизические методы дистанционного зондирования земли, страница 11

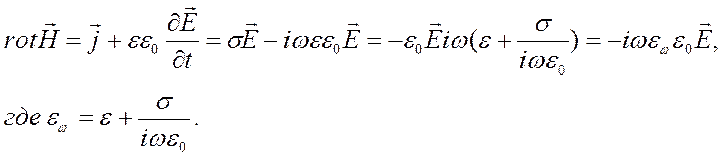
Применение к левой и правой части операции ротора, как и в случае с электромагнитным полем в вакууме приведет к волновому уравнению:

, решением которого является волновая функция.

Отличие результатов заключается в том, что дисперсионное соотношение будет выглядеть так же как в равенстве (1.5.4), но с другим выражением для диэлектрической проницаемости, которая теперь стала комплексной величиной: 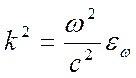    . Волновое число также становится комплексным и его можно представить в виде действительной части k_r  и мнимой –  k_i :

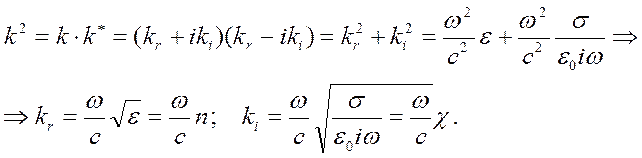     (1.5.5)

В этом случае волновая функция может быть представлена следующим образом: 

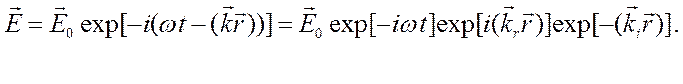
Если направить, как и раньше, волну по оси Oz, то 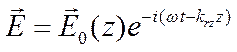, где  . Последнее равенство следует понимать как эффект затухания волны в зависимости от глубины проникновения поля в проводящую среду. Дисперсионное соотношение показывает, что показатель преломления становится комплексной величиной и наблюдается явление дисперсии. В диэлектрике дисперсия связана не с токами проводимости, а с токами смещения, то есть с переменной поляризацией связанных зарядов. Каким образом в веществе возникает дисперсия можно понять, если рассмотреть упрощенную модель взаимодействия упруго связанного электрона с электромагнитным полем.

Будем рассматривать электрон в веществе как одномерный осциллятор, движущийся под действием внутренних квазиупругих сил, пропорциональных смещению x. Выведенный из равновесия электрон на связи начинает излучать при неравномерном движении и потери энергии при излучении можно рассматривать как потери при трении. Эти силы радиационного трения будем считать пропорциональными мгновенной скорости его движения . Наконец, электрон выводится из равновесия под действием внешнего электрического поля электромагнитной волны, направленной по оси Oz с напряженностью E_x в проекции на ось Ox.

.

Изменение электрического поля во времени происходит с частотой ω , а частота собственных колебаний электрона в отсутствии внешних воздействий равна ω₀ . Условие  z≈ 0 означает, что электрон для простоты расчетов выбран вблизи поверхности вещества. Уравнение движения электрона в соответствии со II-м законом Ньютона может быть записано следующим образом:

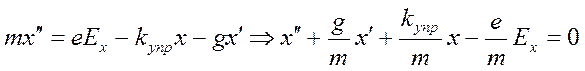 ,    (1.6.1)

где e – величина заряда электрона, k_упр – коэффициент упругости квазиупругих сил, а g – коэффициент радиационного трения. Общее решение уравнения движения электрона может быть представлено в виде суммы двух частных решений, что можно проверить непосредственной подстановкой записанной ниже функции x(t) в основное уравнение (1.6.1).

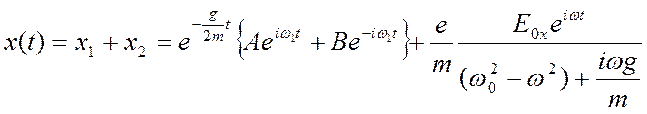,  (1.6.2)

где 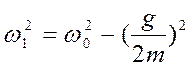   . Частное решение x₁ за счет первого сомножителя приводит к быстрому затуханию колебаний на частоте ω₁ и основной вклад в движение электрона дает второе частное решение. Найдем зависимость коэффициента преломления среды от частоты внешнего электромагнитного поля, используя частное решение x₂. Как известно из электродинамики, вектор индукции электрического поля в среде представляет собой совокупность поляризованного вакуума и среды, поэтому можно записать 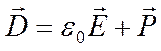, откуда, используя материальные уравнения, имеем:

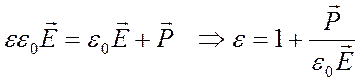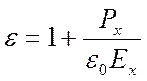 , или переходя к проекции на направление смещения электрона по оси Ox, получаем     . Величина поляризации P_x определяется суммой моментов всех диполей, образованных в единице объема смещением электронов на величину x из положения равновесия. Считая все диполи одинаковыми, и обозначая их количество в единице объема N, получаем: 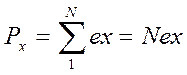 . Для величины диэлектрической проницаемости в этом случае будем иметь:

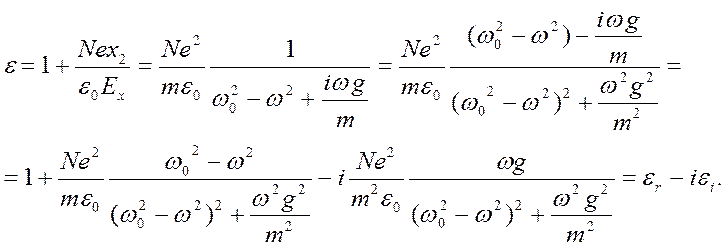
Очевидно, что диэлектрическая проницаемость среды (следовательно, и показатель преломления) оказалась комплексной величиной. График действительной части 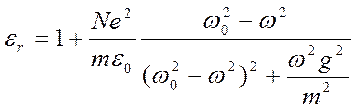        демонстрирует ход кривой явления дисперсии, где четко выражены области нормальной (при ω<< ω₀  и  ω>> ω₀ ) и аномальной (ω ≈ ω₀ ) дисперсии (рис. 4).

Рис. 4. Кривая дисперсии в модели упруго связанного электрона